Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất

Phương pháp giải - Xem chi tiết

Bước 1: Lập công thức tính diện tích hình chữ nhật dưới dạng hàm số

Bước 2: Lập bảng biến thiên của hàm số

Bước 3: Tính diện tích lớn nhất của hình chữ nhật là tìm gía trị lớn nhất của hàm số

Lời giải chi tiết

Gọi x là chiều dài hình chữ nhật (0<x<9)

Khi đó chiều rộng hình chữ nhật là 9 - x ( > 0)

Diện tích hình chữ nhật là S(x) = x( 9 - x )

Ta có \({\rm{S'(x) = 9 - 2x}}\)

Xét \({\rm{S'(x) = 0}}\) \( \Rightarrow {\rm{x = }}\frac{{\rm{9}}}{{\rm{2}}}\)

Ta có bảng biến thiên là

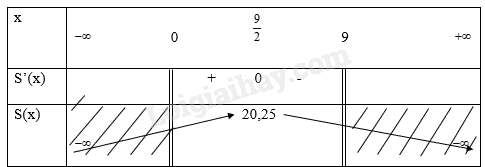
Vậy diện tích lớn nhất của hình chữ nhật là 20,25 khi chiều dài và chiều rộng bằng nhau và bằng \(\frac{{\rm{9}}}{{\rm{2}}}\)

Bài trước Bài sau