Giải bài tập 2 trang 92 SGK Toán 9 tập 1 - Cánh diều

Đề bài

Cho hình thoi \(ABCD\) có \(AB = a,\widehat {BAD} = 2\alpha \left( {0^\circ  < \alpha  < 90^\circ } \right)\). Chứng minh:

a) \(BD = 2a.\sin \alpha \).

b) \(AC = 2a.\cos \alpha \).

Lời giải chi tiết

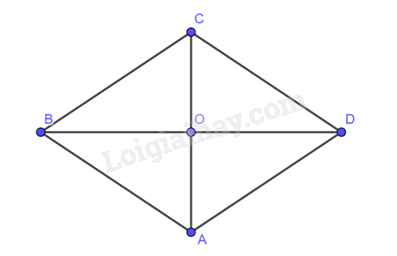
Do \(\widehat {BAD} = 2\alpha\) nên \(\widehat {OAB} = \alpha \).

a) Xét tam giác \(BOA\) vuông tại \(O\) có :

\(BO = AB.\sin \alpha  = a.\sin \alpha \).

Mà \(BD = 2BO = 2a.\sin \alpha \).

b) Xét tam giác \(BOA\) vuông tại \(O\) có:

\(AO = AB.\cos \alpha  = a.\cos \alpha \).

Mà \(AC = 2AO = 2a.\cos \alpha \).