Giải bài tập 2.11 trang 65 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

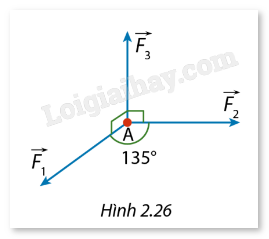
Một chất điểm \(A\) nằm trên mặt phẳng nằm ngang \((\alpha )\), chịu tác động bởi ba lực \({\vec F_1},{\vec F_{{2^\prime }}}{\vec F_3}\). Các lực \({\vec F_1},{\vec F_2}\) có giá nằm trong \((\alpha )\) và \(\left( {{{\vec F}_1},{{\vec F}_2}} \right) = {135^\circ }\), còn lực \({\vec F_3}\) có giá vuông góc với ( \(\alpha \) ) và hướng lên trên. Xác định hợp lực của các lực \({\vec F_1},{\vec F_2},{\vec F_3}\), biết rằng độ lớn của ba lực đó lần lượt là 20N, 15N và 10N.

Lời giải chi tiết

- Độ lớn của hợp lực \({\vec F_1} + {\vec F_2}\) trong mặt phẳng \((\alpha )\) được tính bằng định lý cosin: \({F_{12}} = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos {{135}^\circ }} \)

Thay số liệu:

\({F_{12}} = \sqrt {{{20}^2} + {{15}^2} + 2 \cdot 20 \cdot 15 \cdot \cos {{135}^\circ }} \)

\({F_{12}} = \sqrt {400 + 225 - 600\frac{{\sqrt 2 }}{2}}  = \sqrt {625 - 600\frac{{\sqrt 2 }}{2}}  \approx 14,2{\mkern 1mu} {\rm{N}}\)

Tổng hợp lực của \({\vec F_1} + {\vec F_2}\) và \({\vec F_3}\) là: \(F = \sqrt {F_{12}^2 + F_3^2} \)

Thay số liệu: \(F = \sqrt {14,{2^2} + {{10}^2}}  \approx 17,3{\mkern 1mu} {\rm{N}}\)