-
Toán 9 tập 1
-
Toán 9 tập 2
Giải bài tập 5 trang 78 SGK Toán 9 tập 2 - Cánh diều
Đề bài
Cho hình thang ABCD (AB//CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat C = \widehat D\) (do cùng bù với góc A).
Lời giải chi tiết
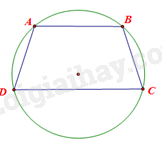
Ta có: ABCD nội tiếp đường tròn nên \(\widehat A + \widehat C = 180^\circ .\) Hơn nữa \(\widehat A + \widehat D = 180^\circ \) (do AB//CD)
Suy ra \(\widehat C = \widehat D\).
Xét hình thang ABCD có AB//CD, \(\widehat C = \widehat D\) nên ABCD là hình thang cân (dhnb).