Giải bài 1 trang 106 vở thực hành Toán 9 tập 2

Đề bài

Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

Phương pháp giải - Xem chi tiết

+ Gọi M là trung điểm của BC.

+ Chứng minh \(ME = MB = MC = MF\). Suy ra đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).

+ Chứng minh tương tự ta có \(CAFD\)và \(ABDE\) cũng là các tứ giác nội tiếp.

Lời giải chi tiết

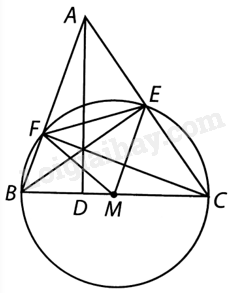
Lấy \(M\) là trung điểm của BC.

Do \(BCE,BCF\) là các tam giác vuông có chung cạnh huyền \(BC\) nên \(ME = MB = MC = MF\).

Do đó đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).

Tương tự, \(CAFD\) và \(ABDE\) cũng là các tứ giác nội tiếp.

Bài trước Bài sau