- Trang chủ
- Lớp 9
- Toán học Lớp 9
- Vở thực hành Toán Lớp 9
- Vở thực hành Toán 9 - Tập 1
- Chương IV. Hệ thức lượng trong tam giác vuông
-
Vở thực hành Toán 9 - Tập 1

-
 Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn
Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn
-
 Chương II. Phương trình và bất phương trình bậc nhất một ẩn
Chương II. Phương trình và bất phương trình bậc nhất một ẩn
-
 Chương III. Căn bậc hai và căn bậc ba
Chương III. Căn bậc hai và căn bậc ba
-
 Chương IV. Hệ thức lượng trong tam giác vuông
Chương IV. Hệ thức lượng trong tam giác vuông
-
 Chương V. Đường tròn
Chương V. Đường tròn
- Bài 13. Mở đầu về đường tròn
- Bài 14. Cung và dây của một đường tròn
- Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Luyện tập chung trang 107
- Bài 16. Vị trí tương đối của đường thẳng và đường tròn
- Bài 17. Vị trí tương đối của hai đường tròn
- Luyện tập chung trang 119
- Bài tập cuối chương V
-
-
Vở thực hành Toán 9 - Tập 2

Giải bài 1 trang 84 vở thực hành Toán 9
Đề bài
Một cuốn sách khổ \(17 \times 24cm\), tức là chiều rộng 17cm, chiều dài 24cm. Gọi \(\alpha \) là góc giữa đường chéo và cạnh 17cm. Tính \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ hai) và tính số đo \(\alpha \) (làm tròn đến độ).
Phương pháp giải - Xem chi tiết
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết
Giả sử ABCD là hình ảnh một trang sách (H.4.23) với \(AB = 17cm,BC = 24cm\), khi đó \(\widehat {BAC} = \alpha \)
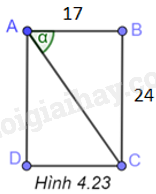
Trong tam giác vuông ABC, ta có
\(A{C^2} = A{B^2} + B{C^2} = {17^2} + {24^2} = 865\) nên \(AC = \sqrt {865} \)
Từ đó, \(\sin \alpha = \frac{{BC}}{{AC}} = \frac{{24}}{{\sqrt {865} }} \approx 0,82\); \(\cos \alpha = \frac{{AB}}{{AC}} = \frac{{17}}{{\sqrt {865} }} \approx 0,58\)
suy ra \(\alpha \approx {55^o}\).