Giải bài 1 trang 98 vở thực hành Toán 9

Đề bài

Trong mặt phẳng tọa độ Oxy, cho các điểm M(0; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O; \(\sqrt 5 \))? Vì sao?

Lời giải chi tiết

(H.5.1)

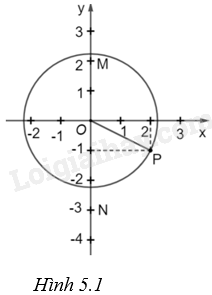
Điểm M(0; 2) nằm trong đường tròn (O; \(\sqrt 5 \)) vì \(OM = 2 < R = \sqrt 5 \).

Điểm N (0; -3) nằm ngoài đường tròn (O; \(\sqrt 5 \)) vì \(ON = 3 > R = \sqrt 5 \).

Điểm P(2; -1) có \(O{P^2} = {1^2} + {2^2} = 5\), tức là \(OP = R = \sqrt 5 \) nên P nằm trên đường tròn (O; \(\sqrt 5 \)).