Giải bài 10 trang 120 SGK Toán 7 tập 2 - Cánh diều

Đề bài

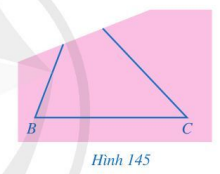
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình?

Phương pháp giải - Xem chi tiết

Vẽ giao điểm của hai đường cao từ đỉnh B, C rồi lấy giao điểm và từ giao điểm đó vẽ đường thẳng vuông góc với BC cắt BC tại D.

Lời giải chi tiết

Trong tam giác, đường có độ dài ngắn nhất luôn là đường cao (đường vuông góc).

Vậy: khoảng cách từ D đến điểm A là nhỏ nhất khi \(AD \bot BC\).

Bước 1: Vẽ hai đường cao hạ từ đỉnh B và C.

Bước 2: Gọi H là giao điểm của hai đường cao.

Bước 3: Vẽ đường cao hạ từ H xuống BC. Và giao điểm của đường cao hạ từ H với đoạn thẳng BC là điểm D ta cần tìm.

Bài trước Bài sau