-
GIẢI SGK TOÁN 8 CÁNH DIỀU - MỚI NHẤT

-
Toán 7 tập 1

-
 Chương I. Số hữu tỉ
Chương I. Số hữu tỉ
-
 Chương II. Số thực
Chương II. Số thực
- Bài 1. Số vô tỉ. Căn bậc hai số học
- Bài 2. Tập hợp R các số thực
- Bài 3. Giá trị tuyệt đối của một số thực
- Bài 4. Làm tròn và ước lượng
- Bài 5. Tỉ lệ thức
- Bài 6. Dãy tỉ số bằng nhau
- Bài 7. Đại lượng tỉ lệ thuận
- Bài 8. Đại lượng tỉ lệ nghịch
- Bài tập cuối chương II
- Hoạt động thực hành và trải nghiệm. Chủ đề 1: Một số hình thức khuyến mãi trong kinh doanh
-
 Chương III. Hình học trực quan
Chương III. Hình học trực quan
-
 Chương IV. Góc. Đường thẳng song song
Chương IV. Góc. Đường thẳng song song
-
-
Toán 7 tập 2

-
 Chương V. Một số yếu tố thống kê và xác suất
Chương V. Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập, phân loại và biểu diễn dữ liệu
- Bài 2. Phân tích và xử lí dữ liệu
- Bài 3. Biểu đồ đoạn thẳng
- Bài 4. Biểu đồ hình quạt tròn
- Bài 5. Biến cố trong một số trò chơi đơn giản
- Bài 6. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài tập cuối chương V
- Hoạt động thực hành và trải nghiệm. Chủ đề 3. Dung tích phổi
-
 Chương VI. Biểu thức đại số
Chương VI. Biểu thức đại số
-
 Chương VII. Tam giác
Chương VII. Tam giác
- Bài 1. Tổng các góc của một tam giác
- Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
- Bài 3. Hai tam giác bằng nhau
- Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
- Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
- Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc
- Bài 7. Tam giác cân
- Bài 8. Đường vuông góc và đường xiên
- Bài 9. Đường trung trực của một đoạn thẳng
- Bài 10. Tính chất ba đường trung tuyến của tam giác
- Bài 11. Tính chất ba đường phân giác của tam giác
- Bài 12. Tính chất ba đường trung trực của tam giác
- Bài 13. Tính chất ba đường cao của tam giác
- Bài tập cuối chương VII
-
Giải bài 2 trang 107 SGK Toán 7 tập 2 - Cánh diều
Đề bài
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN; b) \(\Delta GBC\) cân tại G.
Phương pháp giải - Xem chi tiết
a) Chứng minh BM = CN bằng cách chứng minh tam giác ABM bằng tam giác ACN.
b) Chứng minh \(\Delta GBC\) cân tại G bằng cách chứng minh GB = GC.
Lời giải chi tiết
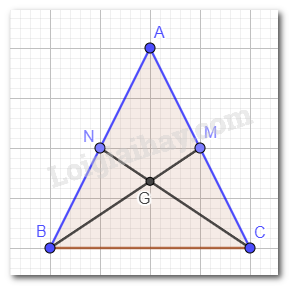
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.