Giải bài 5 trang 117 vở thực hành Toán 9 tập 2

Đề bài

Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như hình bên.

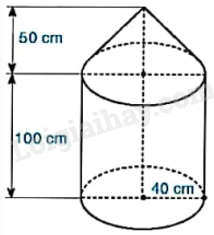
a) Tính thể tích của dụng cụ này.

b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).

Phương pháp giải - Xem chi tiết

a) Thể tích của hình trụ có bán kính đáy R và chiều cao h là: \(V={{S}_{đ\acute{a}y}}.h=\pi {{R}^{2}}h\).

Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).

b) Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).

Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).

Lời giải chi tiết

a) Thể tích của hình trụ là:

\({V_1} = \pi {R^2}h = \pi {.40^2}.100 = 160\;000\pi \left( {c{m^3}} \right).\)

Thể tích của hình nón là:

\({V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.40^2}.50 = \frac{{80\;000\pi }}{3}\left( {c{m^3}} \right).\)

Thể tích của dụng cụ này là:

\(V = {V_1} + {V_2} = 160\;000\pi + \frac{{80\;000\pi }}{3} = \frac{{560\;000\pi }}{3}\left( {c{m^3}} \right).\)

b) Diện tích xung quanh hình trụ là:

\({S_1} = 2\pi Rh = 2\pi \cdot 40 \cdot 100 = 8\,\,000\pi \,\,\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Diện tích xung quanh hình nón là:

\({S_2} = \pi Rl = \pi \cdot 40 \cdot \sqrt {{{40}^2} + {{50}^2}} = 400\sqrt {41} \pi \,\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Diện tích mặt ngoài dụng cụ này là:

\(S = {S_1} + {S_2} = 8{\rm{\;}}000\pi + 400\sqrt {41} \pi \,\,\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Bài trước Bài sau