Giải bài tập 2.4 trang 64 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

Cho hình hộp ABCD.EFGH. Đặt \(\overrightarrow {AB}  = \vec a,\overrightarrow {AD}  = \vec b,\overrightarrow {AE}  = \vec c\). Gọi M là trung điểm của đoạn BG. Hãy biểu diễn \(\overrightarrow {AM} \) theo \(\vec a,\vec b,\vec c\).

Lời giải chi tiết

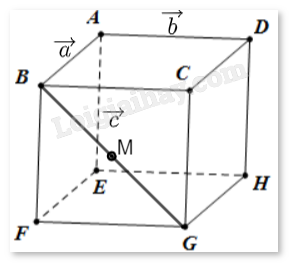
- Áp dụng quy tắc ba điểm, ta có: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM} \)

- Vì M là trung điểm BG nên: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {BG} \)

- Mà ABCD.EFGH là hình hộp nên: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AH}  = \overrightarrow {AB}  + \frac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {AE} } \right) = \overrightarrow a  + \frac{1}{2}\overrightarrow b  + \frac{1}{2}\overrightarrow c \)