Giải bài tập 5.43 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
Đề bài
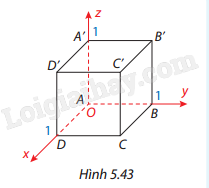
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, với A(0; 0; 0), D(1; 0; 0), B(0; 1; 0), A’(0; 0; 1).
a) Chứng minh \(A'C \bot (AB'D')\).
b) Chứng minh \((AB'D')//(C'BD)\)và tính khoảng cách giữa hai mặt phẳng \((AB'D')\) và \((C'BD)\).
c) Tính côsin của góc giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\).
Phương pháp giải - Xem chi tiết
a) Chứng minh đường thẳng vuông góc với mặt phẳng:
- Tìm véc-tơ pháp tuyến của mặt phẳng bằng tích có hướng của hai véc-tơ trong mặt phẳng.
- Kiểm tra tích vô hướng giữa véc-tơ chỉ phương của đường thẳng và véc-tơ pháp tuyến của mặt phẳng. Nếu tích vô hướng bằng 0, đường thẳng vuông góc với mặt phẳng.
b) Chứng minh hai mặt phẳng song song và tính khoảng cách:
- Tìm véc-tơ pháp tuyến của từng mặt phẳng. Nếu hai véc-tơ pháp tuyến cùng phương, hai mặt phẳng song song.
- Tính khoảng cách giữa hai mặt phẳng song song bằng công thức khoảng cách từ điểm đến mặt phẳng.
c) Tính góc giữa hai mặt phẳng:
- Tìm véc-tơ pháp tuyến của mỗi mặt phẳng.
- Dùng công thức để tính góc giữa hai mặt phẳng.
Lời giải chi tiết
Các đỉnh còn lại có toạ độ là: \(C(1;1;0)\), \(B'(0;1;1)\), \(C'(1;1;1)\), \(D'(1;0;1)\)
a) Chứng minh \(A'C \bot (AB'D')\)
Véc-tơ pháp tuyến của \((AB'D')\):
\(\overrightarrow {AB'} = (0;1;1),\quad \overrightarrow {AD'} = (1;0;1)\)
\({\vec n_{(AB'D')}} = \overrightarrow {AB'} \times \overrightarrow {AD'} = (1;1; - 1)\)
Mà ta có: \(\overrightarrow {A'C} = (1;1; - 1)\)trùng với vec-tơ pháp tuyến của \((AB'D')\)
Vậy \(A'C \bot (AB'D')\).
b) Chứng minh \((AB'D')\parallel (C'BD)\) và tính khoảng cách
Véc-tơ pháp tuyến của \((C'BD)\):
\(\overrightarrow {C'B} = ( - 1;0; - 1),\quad \overrightarrow {C'D} = (0; - 1; - 1)\)
\({\vec n_{(C'BD)}} = \overrightarrow {C'B} \times \overrightarrow {C'D} = ( - 1; - 1;1)\)
Hai véc-tơ pháp tuyến \({\vec n_{(AB'D')}}\) và \({\vec n_{(C'BD)}}\) cùng phương nên \((AB'D')\parallel (C'BD)\).
* Khoảng cách giữa hai mặt phẳng:
Chọn điểm \(A(0,0,0)\) thuộc \((AB'D')\).
Phương trình \((C'BD)\): \(1.(x - 0) - 1.(y - 1) - (z - 0) = 0 \Leftrightarrow x - y - z + 1 = 0\).
\(d = \frac{{|0 \cdot 1 - 0 \cdot 1 - 0 \cdot ( - 1) + 1|}}{{\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {1^2}} }} = \frac{1}{{\sqrt 3 }}\)
c) Tính \(\cos \theta \) giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\)
- Véc-tơ pháp tuyến của \((DA'C')\):
\(\overrightarrow {DA'} = ( - 1;0;1),\quad \overrightarrow {DC'} = (0;1;1)\)
\({\vec n_{(DA'C')}} = \overrightarrow {DA'} \times \overrightarrow {DC'} = ( - 1;1; - 1)\)
Véc-tơ pháp tuyến của \((ABB'A')\):
\(\overrightarrow {AB} = (0,1,0),\quad \overrightarrow {AA'} = (0,0,1)\)
\({\vec n_{(ABB'A')}} = \overrightarrow {AB} \times \overrightarrow {AA'} = (1,0,0)\)
Tính \(\cos \theta \):
\({\vec n_{(DA'C')}} \cdot {\vec n_{(ABB'A')}} = ( - 1;1; - 1) \cdot (1;0;0) = - 1\)
\(\cos \theta = \frac{{| - 1|}}{{\sqrt 3 \cdot 1}} = \frac{1}{{\sqrt 3 }}\)
- Giải bài tập 5.44 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.45 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.46 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.47 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.48 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

