Giải mục 2 trang 12,13,14 SGK Toán 12 tập 1 - Cùng khám phá
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 12 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = \frac{x^2{{} + 4}}{x}\)
a) Xét tính liên tục của hàm số đã cho trên mỗi đoạn\([ - 5; - 1]\) và \([ - 4;3]\)
b) Tính giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của hàm số đã cho trên các đoạn\([ - 5; - 1]\) và \([ - 4;3]\)
Phương pháp giải:
a) Tìm tập xác định của hàm số
b) Bước 1: Tính \(y'\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên các đoạn
Lời giải chi tiết:
a) TXĐ: \(x \in R/\{ 0\} \)
Vậy hàm số liên tục trên đoạn \([ - 5; - 1]\)
Và không liên tục trên đoạn \([ - 4;3]\)
Ta có \(y' = \frac{{{x^2} - 4}}{{{x^2}}}\)
Xét \(y' = 0\) \( \Rightarrow {x^2} - 4 = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Từ đó ta có bảng biến thiên là
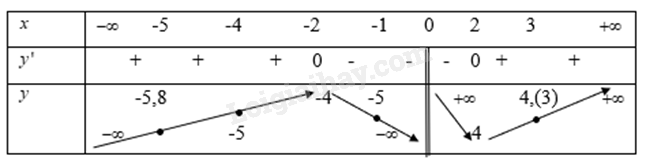
b) Từ bảng biến thiên ta có
Hàm số\ (y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất trên khoảng\([ - 5; - 1]\) tại \(x = 1\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất trên khoảng\([ - 5; - 1]\) tại điểm \(x = - 5\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất \([ - 4;3]\) trên khoảng tại điểm
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất \([ - 4;3]\) trên khoảng tại điểm
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 13 SGK Toán 12 Cùng khám phá
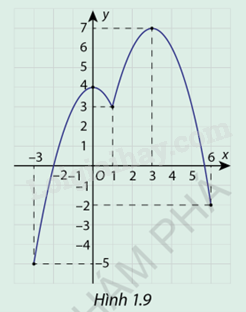
Cho hàm số \(y = f(x)\) liên tục trên đoạn, có đạo hàm trên các khoảng \(( - 3;1)\)và \((1;6)\) có dồ thị hàm số như hình 1.9, biết rằng \(f( - 3) = - 5\) và \(f(6) = - 2\)
a) Xác định các điểm cực trị thuộc đoạn \([ - 3;6]\) của hàm số
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \([ - 3;6]\)
Phương pháp giải:
Dựa vào đồ thị hàm số (hình 1.9) rồi nhận xét
Lời giải chi tiết:
a) Dựa vào đồ thị hàm số, ta thấy
Đồ thị hàm số có các điểm cực trị là \(x = - 3\), \(x = 0\), \(x = 1\),\(x = 3\), \(x = 6\)
b) Hàm số đạt giá trị lớn nhất trên khoảng \([ - 3;6]\) tại \(x = 3\)
Hàm số đạt giá trị nhỏ nhất trên khoảng \([ - 3;6]\) tại \(x = - 3\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 14 SGK Toán 12 Cùng khám phá
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \frac{{x + 2}}{{x - 1}}\) trên đoạn \([2;4]\)
Phương pháp giải:
Bước 1 Tính \(y'\)
Bước 2 Lập bảng biến thiên
Bước 3 Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số trên đoạn \([2;4]\)
Lời giải chi tiết:
Hàm số trên xác định trên R/{1}
Ta có \(y' = \frac{{ - 3}}{{{{(x - 1)}^2}}}\)
Vì \(y' < 0\) với \(x \in R/\{ 1\} \)
Nên hàm số luôn nghịch biến
Khi đó ta có bảng biến thiên là
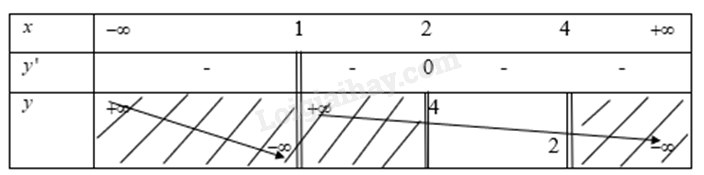
Từ bảng biến thiên ta thấy
Hàm số y đạt giá trị lớn nhất tại x = 2 khi đó y = 4
Hàm số y đạt giá trị lớn nhất tại x = 4 khi đó y = 2
- Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.10 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.13 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

