- Trang chủ
- Lớp 11
- Toán học Lớp 11
- SGK Toán Lớp 11 Cánh diều
- Toán 11 tập 1 - Cánh Diều Cánh diều
- Chương 4 Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
Toán 11 tập 1 - Cánh Diều

-
Giải Toán 11 tập 2 - Cánh Diều

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Đề bài
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho \(AD = 3AM\). Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).
Lời giải chi tiết
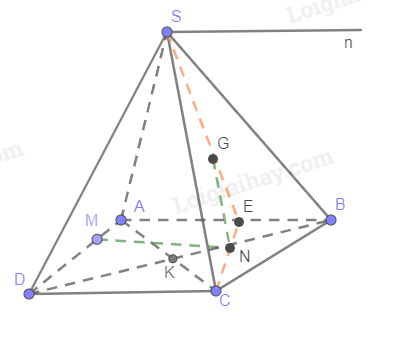
+Ta có: \(KN = \frac{1}{3}KB = \frac{1}{6}DB\)
Tam giác DAB có: \(\frac{{DN}}{{DB}} = \frac{{DK + KN}}{{DB}} = \frac{{\frac{1}{2}DB + \frac{1}{6}DB}}{{DB}} = \frac{2}{3} = \frac{{DM}}{{DA}}\)
Theo Ta lét, suy ra MN // AB mà AB // CD
Suy ra MN // CD mà CD \( \subset \)(SCD) nên MN // (SCD).
+ Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)
