- Trang chủ
- Lớp 9
- Toán học Lớp 9
- Vở thực hành Toán Lớp 9
- Vở thực hành Toán 9 - Tập 1
- Chương V. Đường tròn
-
Vở thực hành Toán 9 - Tập 1

-
 Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn
Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn
-
 Chương II. Phương trình và bất phương trình bậc nhất một ẩn
Chương II. Phương trình và bất phương trình bậc nhất một ẩn
-
 Chương III. Căn bậc hai và căn bậc ba
Chương III. Căn bậc hai và căn bậc ba
-
 Chương IV. Hệ thức lượng trong tam giác vuông
Chương IV. Hệ thức lượng trong tam giác vuông
-
 Chương V. Đường tròn
Chương V. Đường tròn
- Bài 13. Mở đầu về đường tròn
- Bài 14. Cung và dây của một đường tròn
- Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Luyện tập chung trang 107
- Bài 16. Vị trí tương đối của đường thẳng và đường tròn
- Bài 17. Vị trí tương đối của hai đường tròn
- Luyện tập chung trang 119
- Bài tập cuối chương V
-
-
Vở thực hành Toán 9 - Tập 2

Giải bài 1 trang 102 vở thực hành Toán 9
Đề bài
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}\).
Phương pháp giải - Xem chi tiết
+ Gọi H là giao điểm của đường vuông góc hạ từ M xuống AB, M’ là điểm đối xứng với M qua AB.
+ Chứng minh M’ thuộc đường tròn đường kính AB nên MM’ là một dây của đường tròn đường kính AB.
+ Do đó, \(MM' \le AB\) hay \(2MH \le AB\), suy ra \(MH \le \frac{{AB}}{2}\).
Lời giải chi tiết
(H.5.9)
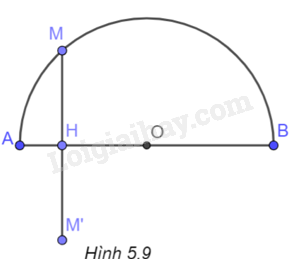
Gọi H là giao điểm của đường vuông góc hạ từ M xuống AB. Khi đó, độ dài đoạn MH là khoảng cách từ M đến AB. Gọi M’ là điểm đối xứng với M qua AB. Khi đó, H là trung điểm của MM’, tức là \(MM' = 2MH\). Mặt khác do AB là đường kính của đường tròn nên M’ thuộc đường tròn đường kính AB. Suy ra MM’ là một dây của đường tròn. Do đó, \(MM' \le AB\) hay \(2MH \le AB\), suy ra \(MH \le \frac{{AB}}{2}\).
Vậy khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}\).