Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo
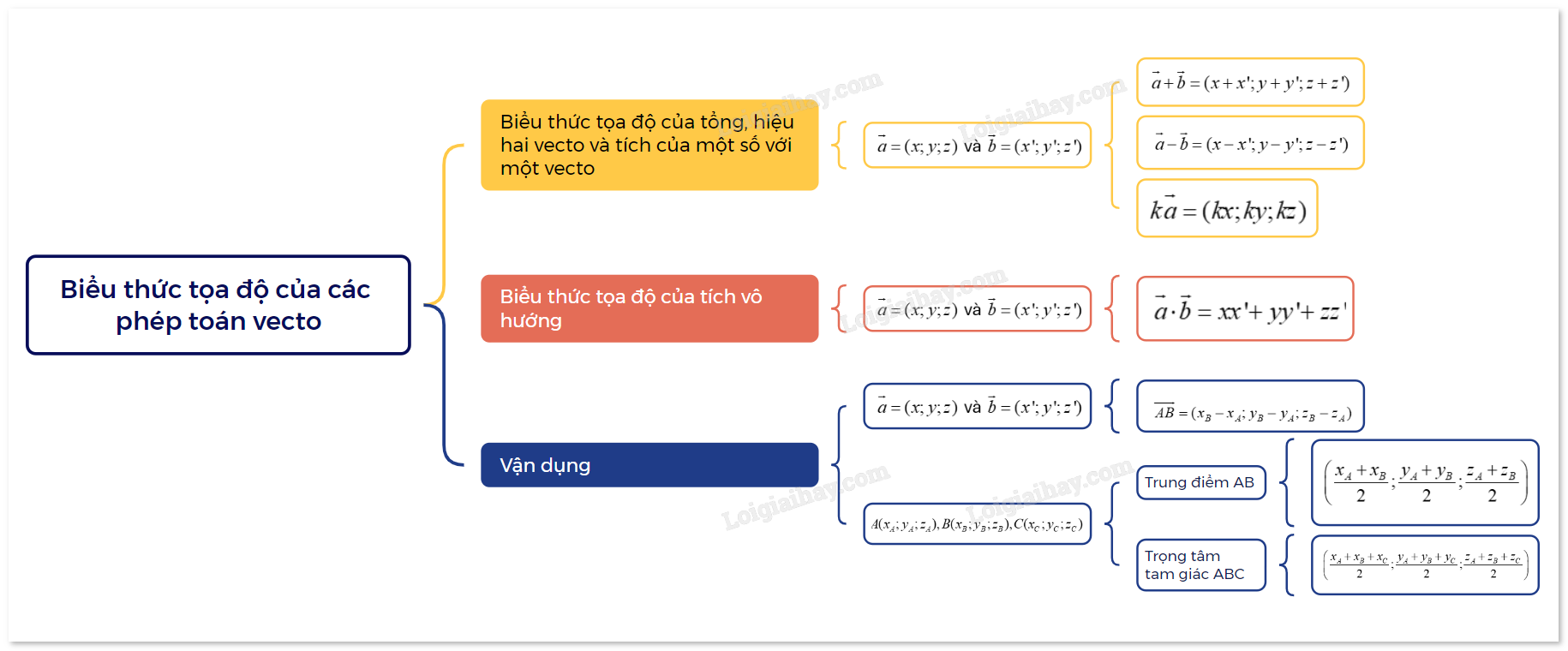
1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto
| Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\). Ta có:
|
2. Biểu thức tọa độ của tích vô hướng
| Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = xx' + yy' + zz'\) |
3. Vận dụng
a) Xác định tọa độ của vecto khi biết tọa độ điểm đầu và điểm cuối
| Trong không gian Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Ta có: \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\) |
b) Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác
| Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Khi đó:
|
- Giải mục 1 trang 58,59 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải mục 2 trang 59,60 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải mục 3 trang 60,61,62 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 1 trang 64 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 64 SGK Toán 12 tập 1 - Chân trời sáng tạo

