- Trang chủ
- Lớp 11
- Toán học Lớp 11
- SGK Toán Lớp 11 Cánh diều
- Toán 11 tập 1 - Cánh Diều Cánh diều
- Chương 4 Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
Toán 11 tập 1 - Cánh Diều

-
Giải Toán 11 tập 2 - Cánh Diều

Bài 5 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Phương pháp giải - Xem chi tiết
Dùng định lí Thales đảo và tính chất đường trung bình tam giác.
Lời giải chi tiết
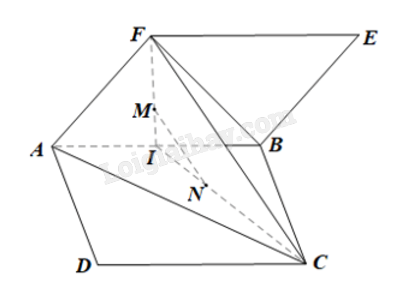
Gọi I là trung điểm của AB.
M là trọng tâm tam giác ABF suy ra \(\frac{{IM}}{{IF}} = \frac{1}{3}\).
N là trọng tâm tam giác ABC suy ra \(\frac{{IN}}{{IC}} = \frac{1}{3}\).
Xét tam giác ICF có \(\frac{{IM}}{{IF}} = \frac{{IN}}{{IC}} = \frac{1}{3}\) suy ra MN//FC (định lí Thales đảo).
Mà FC thuộc mặt phẳng (AFC) suy ra MN//(AFC).
