- Trang chủ
- Lớp 7
- Toán học Lớp 7
- SGK Toán Lớp 7 Kết nối tri thức
- Toán 7 tập 1 với cuộc sống Kết nối tri thức
- Chương II. Số thực
-
GIẢI SGK TOÁN 8 KẾT NỐI TRI THỨC - MỚI NHẤT

-
Toán 7 tập 1 với cuộc sống

-
 Chương I. Số hữu tỉ
Chương I. Số hữu tỉ
-
 Chương II. Số thực
Chương II. Số thực
-
 Chương III. Góc và đường thẳng song song
Chương III. Góc và đường thẳng song song
-
 Chương IV. Tam giác bằng nhau
Chương IV. Tam giác bằng nhau
- Bài 12. Tổng các góc trong một tam giác
- Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
- Luyện tập chung trang 68
- Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác
- Luyện tập chung trang 74
- Bài 15. Các trường hợp bằng nhau của tam giác vuông
- Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng
- Luyện tập chung trang 85
- Bài tập cuối chương IV
-
 Chương V. Thu thập và biểu diễn dữ liệu
Chương V. Thu thập và biểu diễn dữ liệu
-
 Hoạt động thực hành trải nghiệm
Hoạt động thực hành trải nghiệm
-
-
Toán 7 tập 2 với cuộc sống

-
 Chương VI. Tỉ lệ thức và đại lượng tỉ lệ
Chương VI. Tỉ lệ thức và đại lượng tỉ lệ
-
 Chương VII. Biểu thức đại số và đa thức một biến
Chương VII. Biểu thức đại số và đa thức một biến
-
 Chương VIII. Làm quen với biến cố và xác suất của biến cố
Chương VIII. Làm quen với biến cố và xác suất của biến cố
-
 Chương IX. Quan hệ giữa các yếu tố trong tam giác
Chương IX. Quan hệ giữa các yếu tố trong tam giác
- Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 32. Quan hệ giữa đường vuông góc và đường xiên
- Bài 33. Quan hệ giữa ba cạnh của một tam giác
- Luyện tập chung trang 70
- Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Luyện tập chung trang 82
- Bài tập cuối chương IX
-
 Chương X. Một số hình khối trong thực tiễn
Chương X. Một số hình khối trong thực tiễn
-
 Hoạt động thực hành trải nghiệm tập 2
Hoạt động thực hành trải nghiệm tập 2
-
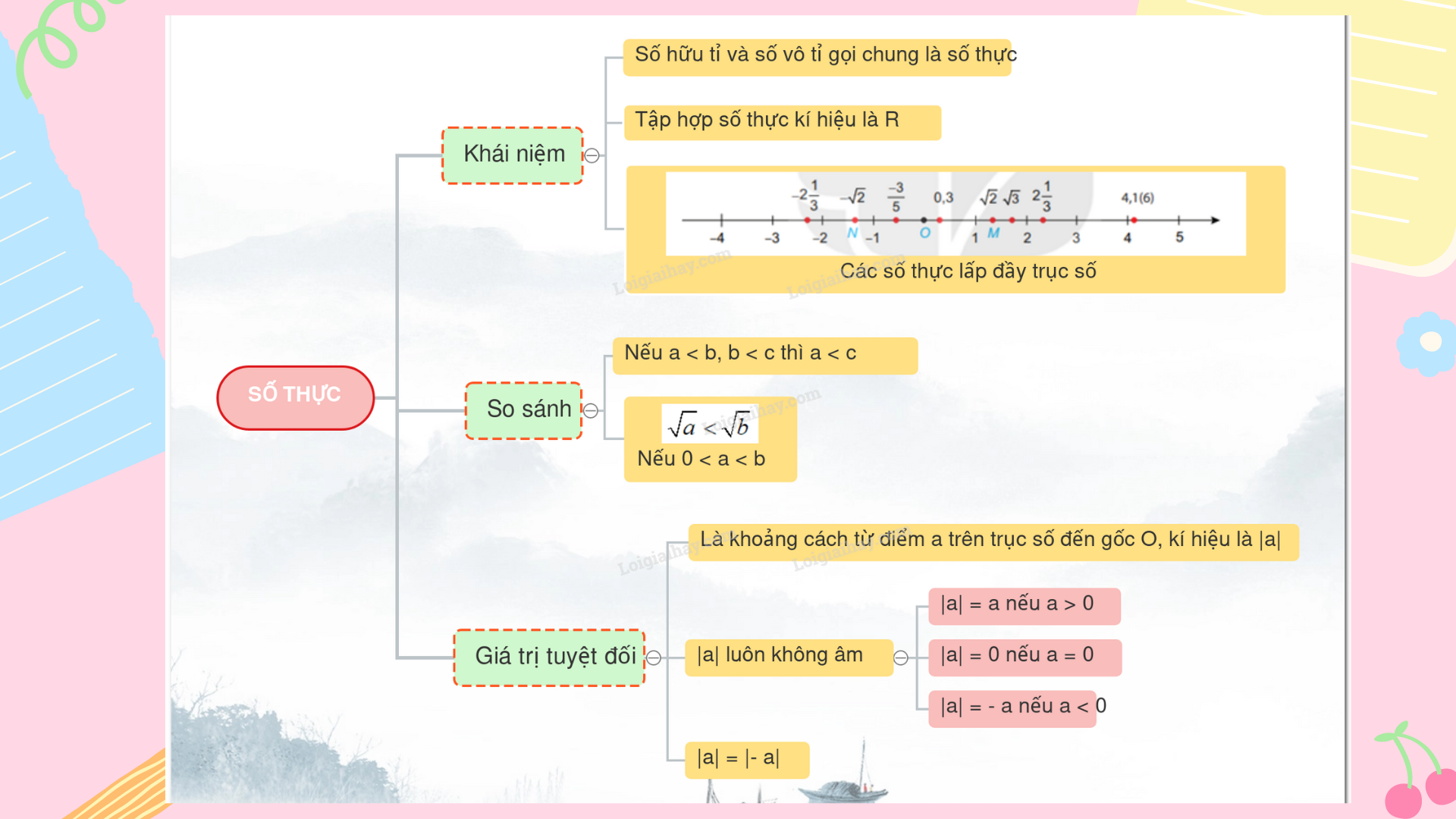
Lý thuyết Tập hợp các số thực SGK Toán 7 - Kết nối tri thức
1. Khái niệm số thực và trục số thực
* Số hữu tỉ và số vô tỉ gọi chung là số thực
* Tập hợp các số thực được kí hiệu là R.
Chú ý: + Mỗi số thực a đều có một số đối là –a
+ Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
* Trục số thực được biểu diễn bởi 1 số điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
Chú ý: Các số thực lấp đầy trục số.
2. Thứ tự trong tập hợp các số thực
a) So sánh 2 số thực:
* Các số thực đều viết được dưới dạng số thập phân ( hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.
Ví dụ:
0,322 … < 0,324… nên 0,3(2) < 0,324…
* Với 2 số thực bất kì, ta luôn có hoặc a = b hoặc a > b hoặc a < b
* Nếu a < b ; b < c thì a < c ( Tính chất bắc cầu)
* Nếu a < b thì điểm a nằm trước điểm b trên trục số
Chú ý: Nếu 0 < a < b thì \(\sqrt a < \sqrt b \)
Ví dụ: Vì 3 < 4 nên \(\sqrt 3 < \sqrt 4 = 2\)
3. Giá trị tuyệt đối của một số thực
Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là |a|
Nhận xét:
+ Hai số đối nhau thì có giá trị tuyệt đối bằng nhau
+ Giá trị tuyệt đối của 0 là 0
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
+ Giá trị tuyệt đối của một số thực luôn không âm.
Ví dụ: |2,3| = 2,3
|-2,3| = 2,3
|-2,3| = |2,3|