- Trang chủ
- Lớp 9
- Toán học Lớp 9
- SGK Toán Lớp 9 Kết nối tri thức
- Toán 9 tập 2 Kết nối tri thức
- Chương 7. Tần số và tần số tương đối
-
Toán 9 tập 1

-
 Chương 1. Phương trình và hệ hai phương trình bậc nhất hai ẩn
Chương 1. Phương trình và hệ hai phương trình bậc nhất hai ẩn
-
 Chương 2. Phương trình và bất phương trình bậc nhất một ẩn
Chương 2. Phương trình và bất phương trình bậc nhất một ẩn
-
 Chương 3. Căn bậc hai và căn bậc ba
Chương 3. Căn bậc hai và căn bậc ba
-
 Chương 4. Hệ thức lượng trong tam giác vuông
Chương 4. Hệ thức lượng trong tam giác vuông
-
 Chương 5. Đường tròn
Chương 5. Đường tròn
- Bài 13. Mở đầu về đường tròn
- Bài 14. Cung và dây của một đường tròn
- Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Luyện tập chung trang 96
- Bài 16. Vị trí tương đối của đường thẳng và đường tròn
- Bài 17. Vị trí tương đối của hai đường tròn
- Luyện tập chung trang 108
- Bài tập cuối chương 5
-
 Hoạt động thực hành trải nghiệm
Hoạt động thực hành trải nghiệm
-
-
Toán 9 tập 2

-
 Chương 6. Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn
Chương 6. Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn
-
 Chương 7. Tần số và tần số tương đối
Chương 7. Tần số và tần số tương đối
-
 Chương 8. Xác suất của biến cố trong một số mô hình xác suất đơn giản
Chương 8. Xác suất của biến cố trong một số mô hình xác suất đơn giản
-
 Chương 9. Đường tròn ngoại tiếp và đường tròn nội tiếp
Chương 9. Đường tròn ngoại tiếp và đường tròn nội tiếp
-
 Chương 10. Một số hình khối trong thực tiễn
Chương 10. Một số hình khối trong thực tiễn
-
 Hoạt động thực hành trải nghiệm
Hoạt động thực hành trải nghiệm
-
 Bài tập ôn tập cuối năm
Bài tập ôn tập cuối năm
-
Giải bài tập 7.30 trang 55 SGK Toán 9 tập 2 - Kết nối tri thức
Đề bài
Lương của các công nhân một nhà máy được cho trong bảng sau:

a) Nêu các nhóm số liệu và tần số. Giải thích ý nghĩa cho một nhóm số liệu và tần số của nó.
b) Vẽ biểu đồ tần số tương đối dạng cột cho bảng thống kê trên.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vẽ biểu đồ tần số tương đối dạng cột:
+ Tính tần số tương đối của các nhóm số liệu.
+ Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột:
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu, mỗi hình cột có chiều cao bằng tần số tương đối của nhóm số liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
Lời giải chi tiết
a) Các nhóm số liệu về tiền lương \(\left[ {5;7} \right)\); \(\left[ {7;9} \right)\); \(\left[ {9;11} \right)\); \(\left[ {11;13} \right)\); \(\left[ {13;15} \right)\) có tần số lần lượt là 20; 50; 70; 40; 20.
Giải thích ý nghĩa của một nhóm số liệu: Nhóm \(\left[ {5;7} \right)\) có tần số là 20 tức là có 20 công nhân có lương từ 5 triệu đến dưới 7 triệu.
b) Tổng số công nhân là: \(20 + 50 + 70 + 40 + 20 = 200\) (công nhân)
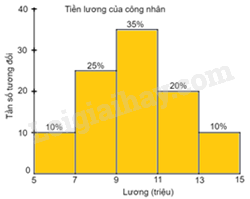
Tần số tương đối của công nhân có lương \(\left[ {5;7} \right)\); \(\left[ {7;9} \right)\); \(\left[ {9;11} \right)\); \(\left[ {11;13} \right)\); \(\left[ {13;15} \right)\) lần lượt là: \(\frac{{20}}{{200}} = 10\% ;\frac{{50}}{{200}} = 25\% ;\frac{{70}}{{200}} = 35\% ;\frac{{40}}{{200}} = 20\% ;\frac{{20}}{{200}} = 10\% \)
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu.
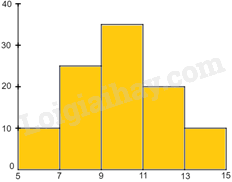
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.