Giải bài 2 (9.32) trang 84 vở thực hành Toán 7 tập 2

Đề bài

Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Phương pháp giải - Xem chi tiết

+ Gọi giao của BN và CM là F thì \(BN \bot CM\) tại F.

+ Chứng minh B là trục tâm của tam giác MNC, suy ra BM là đường cao của tam giác MNC, suy ra BM vuông góc với CN.

Lời giải chi tiết

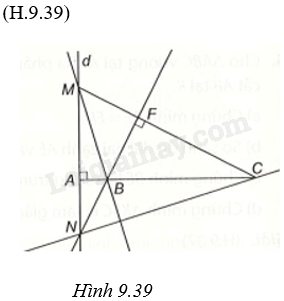
Gọi giao của BN và CM là F thì \(BN \bot CM\) tại F.

Trong tam giác MNC có \(CA \bot MN\)(vì \(d \bot AB\) tại A), \(NF \bot MC\), AC giao với NF tại B nên B là trực tâm của tam giác MNC.

Suy ra BM là đường cao của tam giác MNC hay BM vuông góc với đường thẳng CN.

Bài trước Bài sau