Giải bài 4 trang 70, 71 vở thực hành Toán 7 tập 2

Đề bài

Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD.

a) So sánh BK, BD.

b) So sánh \(BK + CN\) với BC.

c) Chứng minh \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).

Lời giải chi tiết

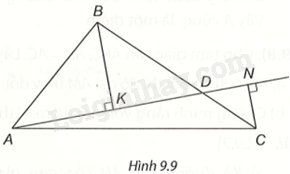
a) Trong tam giác vuông BKD có BD là cạnh huyền nên \(BK < BD\) (1)

b) Từ (1) suy ra \(BK + CN < BD + CN\) (2)

Trong tam giác vuông CND có DC là cạnh huyền nên \(NC < CD\), suy ra: \(BD + CN < BD + CD\). (3)

Từ (2) và (3) suy ra \(BK + CN < BD + CN < BD + CD = BC\).

Do đó, \(BK + CN < BC\). (4)

c) Trong tam giác vuông ABK có AB là cạnh huyền nên \(BK < AB\). (5)

Trong tam giác vuông CAN có AC là cạnh huyền nên \(CN < AC\). (6)

Từ (4), (5) và (6) suy ra \(\left( {BK + CN} \right) + BK + CN < BC + AB + AC\), hay \(2\left( {BK + CN} \right) < AB + BC + CA\), do đó \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).