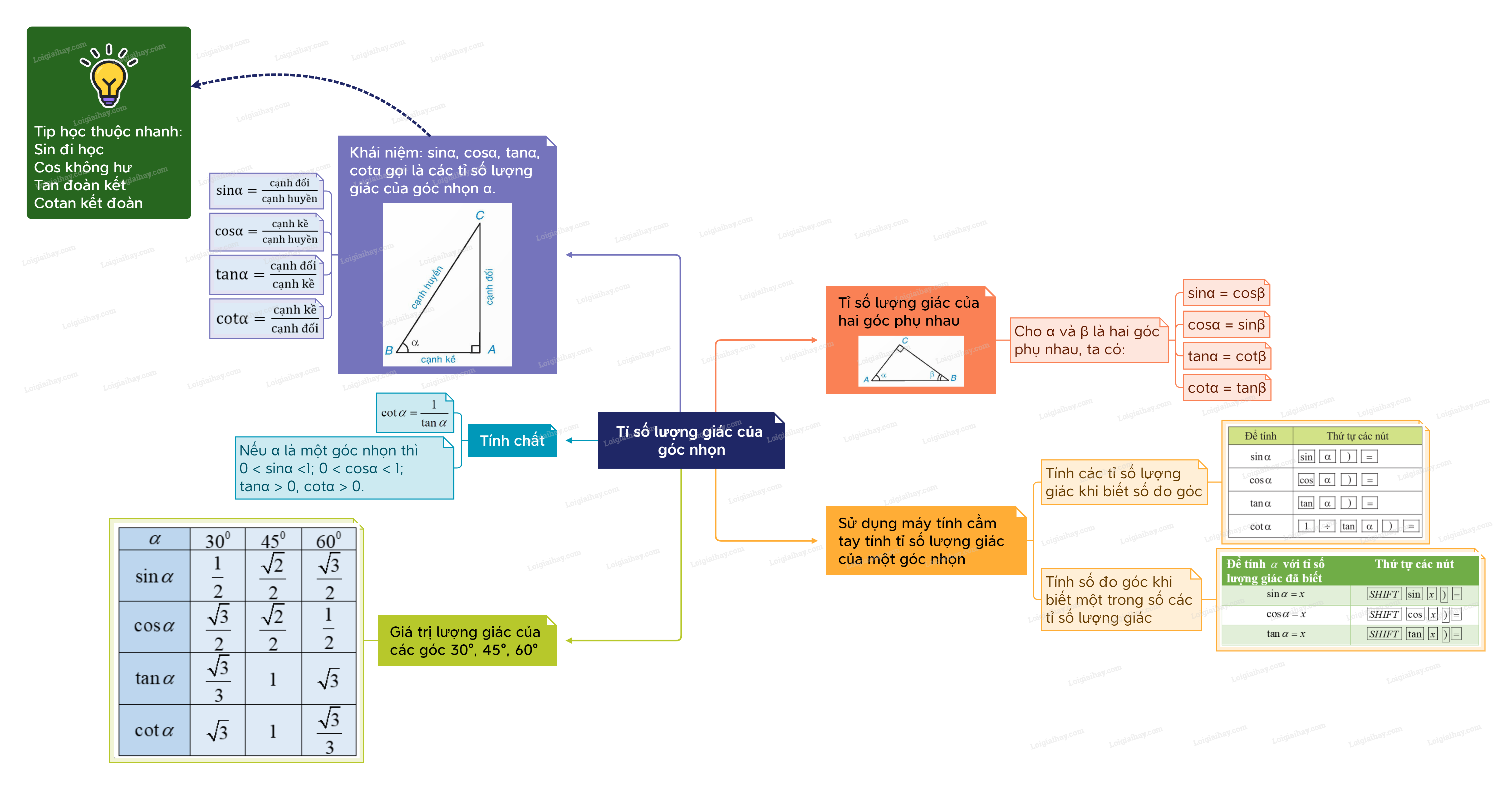
Lý thuyết Tỉ số lượng giác của góc nhọn Toán 9 Kết nối tri thức

1. Khái niệm tỉ số lượng giác của một góc nhọn

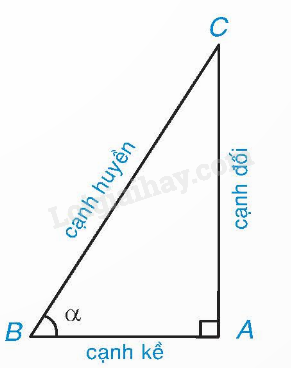
\({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\cot \alpha  = \frac{1}{{\tan \alpha }}\). \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \).

Tip học thuộc nhanh:

Sin đi học Cos không hư Tan đoàn kết Cotan kết đoàn

Chú ý: Nếu \(\alpha \) là một góc nhọn thì \(0 < \sin \alpha  < 1\); \(0 < \cos \alpha  < 1\); \(\tan \alpha  > 0\); \(\cot \alpha  > 0.\)

Ví dụ:

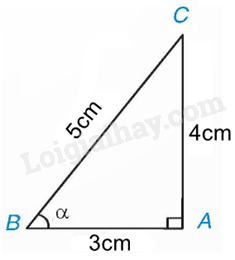
Theo định nghĩa của tỉ số lượng giác, ta có:

\(\sin \alpha  = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha  = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha  = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha  = \frac{{AB}}{{AC}} = \frac{3}{4}\)

Giá trị lượng giác của các góc \({30^0},{45^0},{60^0}\)

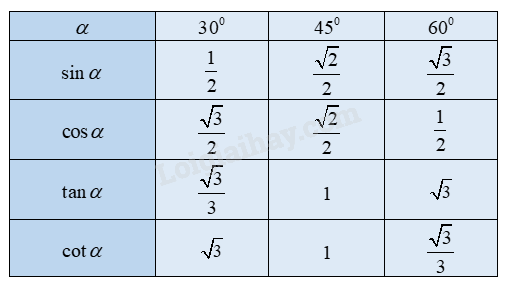
2. Tỉ số lượng giác của hai góc phụ nhau

Định lí về tỉ số lượng giác của hai góc phụ nhau

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtang góc kia.

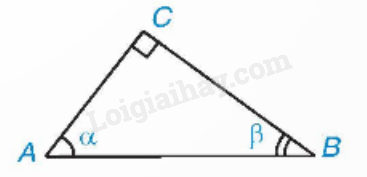
Cho \(\alpha \) và \(\beta \) là hai góc phụ nhau, ta có:

\(\sin \alpha  = \cos \beta \), \(\cos \alpha  = \sin \beta \), \(\tan \alpha  = \cot \beta \), \(\cot \alpha  = \tan \beta \).

Ví dụ:

\(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30' = \sin \left( {{{90}^0} - {{52}^0}30'} \right) = \sin {37^0}30';\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\)

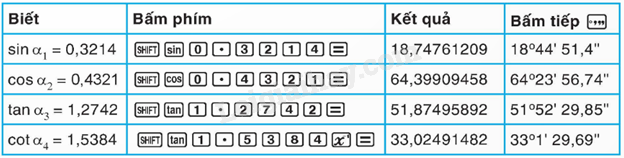
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

Sử dụng máy tính cầm tay để tính các tỉ số lượng giác

Sử dụng máy tính cầm tay để tìm được góc khi biết một trong các tỉ số lượng giác của góc đó

Một số công thức mở rộng:

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)