Giải 1. Bài 1: Tập hợp các số hữu tỉ Toán học Lớp 7 | Hướng Dẫn Giải Kết nối tri thức Chi Tiết

Đề bài

Câu 1

Tập hợp các số hữu tỉ được kí hiệu là:

$\mathbb{R}$
$\mathbb{Q}$
$\mathbb{I}$
$\mathbb{N}$

Câu 2

Số $\dfrac{9}{4}$ có số đối là:

$\dfrac{4}{9}$
$\dfrac{{ - 4}}{9}$
$\dfrac{9}{{ - 4}}$
$2,25$

Câu 3

Khẳng định nào sau đây là đúng?

Nếu a > b thì –a > - b
Nếu a < b, a < c thì b < c
Nếu a < b; c > b thì a < c
Số hữu tỉ gồm: số hữu tỉ dương và số hữu tỉ âm

Câu 4

Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35

$ - \frac{3}{5}$
$\frac{7}{{20}}$
- $\frac{7}{{20}}$
$\frac{{ - 35}}{{10}}$

Câu 5

Biểu diễn các số: $ - 0,4;\frac{8}{{20}};\frac{{12}}{{ - 20}};\frac{{ - 3}}{8}; - 0,375$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?

Câu 6

Sắp xếp các số hữu tỉ $\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$ theo thứ tự giảm dần:

$\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}};\frac{{ - 7}}{{20}}$
$\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}$
$\frac{{ - 7}}{{20}};\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}}$
$\frac{1}{{ - 3}};\frac{{ - 5}}{{17}};\frac{5}{{ - 20}};\frac{{ - 7}}{{20}}$

Câu 7

Cho $x = \frac{a}{{2{a^2} + 1}}$

Với giá trị nào của a thì x là số hữu tỉ dương?

a < 0
a > 0
a = 0
a$ \ge $0

Câu 8

Có mấy giá trị x nguyên thỏa mãn: $\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}$

Câu 9

Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; $\frac{1}{3}$phút; $\frac{{108}}{5}$ giây; $20\frac{3}{8}$ giây.

Hỏi bạn nào chạy nhanh nhất?

An
Bình
Chi
Duy

Câu 10

Cho số hữu tỉ $x = \frac{7}{{n + 2}}$

Tìm tổng của các số nguyên n sao cho x là một số nguyên

-4
4
0
-8

Câu 11

Cho số hữu tỉ $y = \dfrac{{2a - 1}}{{ - 3}}.$ Với giá trị nào của $a$ thì $y$ không là số dương và cũng không là số âm.

$1$
$\dfrac{1}{2}$
$2$
$4$

Câu 12

Cho số hữu tỉ $x = \dfrac{{a - 3}}{2}.$ Với giá trị nào của $a$ thì $x$ là số nguyên dương;

$\dfrac{1}{2}$
$2$
$2021$
$4$

Câu 13

Trong các phân số $\dfrac{{14}}{{18}}\,\,;\,\,\dfrac{{24}}{{26}}\,\,;\,\,\dfrac{{26}}{{ - 28}}\,\,;\,\,\dfrac{{ - 28}}{{30}}\,\,;\,\,\dfrac{{72}}{{78}}$ có bao nhiêu phân số bằng phân số $\dfrac{{12}}{{13}}$ ?

$a = 3 - 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 3 + k\,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 2k\,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)$

Câu 14

Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?

$a = 5 - 7k\,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 5 + 7k\,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 7k-5 \,\left( {k \in {\mathbb{N}^*}} \right)$
$a = 5 - k\,\left( {k \in {\mathbb{N}^*}} \right)$

Câu 15

So sánh $x = \dfrac{{2002}}{{2003}}$ và $y = \dfrac{{14}}{{13}}$

Câu 16

So sánh hai số $x = \dfrac{2}{{ - 5}}$ và $y = \dfrac{{ - 3}}{{13}}$

Câu 17

Số hữu tỉ lớn nhất trong các số $\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}$ là:

1 điểm
4 điểm
3 điểm
2 điểm

Câu 18

Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: $\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.$

$5$ điểm
$4$ điểm
$3$ điểm
$2$ điểm

Câu 19

Cho các câu sau:

(I) Số hữu tỉ dương lớn hơn số hữu tỉ âm

(II) Số hữu tỉ dương lớn hơn số tự nhiên

(III) Số $0$ là số hữu tỉ âm

(IV) Số nguyên dương là số hữu tỉ.

Số các câu đúng trong các câu trên là

$y = x$
$y < x$
$y > x$
$x \ge y$

Câu 20

Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?

$x \ge y$
$y \ge x$
$x>y$
$x < y$

Câu 21

Số $ - \dfrac{2}{3}$ được biểu diễn trên trục số bởi hình vẽ nào dưới đây?

$x > y$
$x < y$
$x = y$
$x \ge y$

Câu 22

Số nào dưới đây là số hữu tỉ dương?

$a > b$
$a < b$
$a = b$
$a \le b$

Câu 23

Chọn câu đúng

$\dfrac{7}{8}$
$\dfrac{3}{4}$
$\dfrac{{18}}{{19}}$
$\dfrac{{27}}{{28}}$

Câu 24

Số hữu tỉ là số được viết dưới dạng phân số $\dfrac{a}{b}$ với:

$\dfrac{5}{6}$
$\dfrac{8}{9}$
$\dfrac{{29}}{{30}}$
$\dfrac{{25}}{{26}}$

Đáp án

Câu 1

Tập hợp các số hữu tỉ được kí hiệu là: Q

Đáp án đúng là b

Câu 2

Số đối của $\dfrac{9}{4}$ là $ - \dfrac{9}{4} = \dfrac{9}{{ - 4}}$

Đáp án đúng là c

Câu 3

+) Nếu a > b thì –a < -b nên A sai

+) Nếu a < b, a < c thì chưa thể so sánh được b với c nên B sai

+) Nếu a < b, c > b ( hay b < c) thì a < c ( tính chất bắc cầu) nên C đúng

+) Số hữu tỉ gồm: số hữu tỉ âm, số hữu tỉ dương và số 0 nên D sai.

Đáp án đúng là c

Câu 4

Ta có:

$ - 0,35 = \frac{{ - 35}}{{100}} = \frac{{( - 35):5}}{{100:5}} = \frac{{ - 7}}{{20}}$

Đáp án đúng là c

Câu 5

Ta có:

$\begin{array}{l} - 0,4 = \frac{{ - 4}}{{10}} = \frac{{ - 4:2}}{{10:2}} = \frac{{ - 2}}{5};\\\frac{8}{{20}} = \frac{{8:4}}{{20:4}} = \frac{2}{5};\\\frac{{12}}{{ - 20}} = \frac{{12:( - 4)}}{{( - 20):( - 4)}} = \frac{{ - 3}}{5};\\\frac{{ - 3}}{8};\\ - 0,375 = \frac{{ - 375}}{{1000}} = \frac{{( - 375):125}}{{1000:125}} = \frac{{ - 3}}{8}\end{array}$

Ta có các điểm biểu diễn khác nhau là $\frac{{ - 2}}{5}; \frac{2}{5}; \frac{{ - 3}}{5}; \frac{{ - 3}}{8}$

Vậy các số trên biểu diễn 4 số hữu tỉ khác nhau nên được biểu diễn bởi 4 điểm khác nhau trên trục số

Đáp án đúng là b

Câu 6

+ So sánh $\frac{5}{{ - 20}}$ và $ \frac{{ - 5}}{{17}}$:

Vì 20 > 17 nên $\frac{5}{{20}} < \frac{5}{{17}}$, do đó $\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}$

+ So sánh $\frac{ - 5}{17}$ và $\frac{1}{{ - 3}}$:

Vì $\frac{5}{{17}} < \frac{5}{{15}}$ nên $\frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}$

+ So sánh $\frac{1}{ - 3}$ và $\frac{{ - 7}}{{20}}$:

Vì $\frac{7}{{20}} > \frac{7}{{21}}$ nên $\frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}$

Do đó, $\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}$

Đáp án đúng là a

Câu 7

Ta có:

a² $ \ge $0, với mọi a nên 2a² + 1 $ \ge $1 > 0, với mọi a

Như vậy, để $x = \frac{a}{{2{a^2} + 1}}$ > 0 thì a > 0

Đáp án đúng là b

Câu 8

Ta có:

$\begin{array}{l}\frac{{9}}{{ - 21}} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \Leftrightarrow \frac{{ - 3}}{7} > \frac{x}{7} > \frac{{ - 11}}{{14}}\\ \Leftrightarrow \frac{{ - 6}}{{14}} > \frac{{2x}}{{14}} > \frac{{ - 11}}{{14}}\\ \Rightarrow - 6 > 2x > - 11\\ \Leftrightarrow - 3 > x > - \frac{{11}}{2}\end{array}$

$ \Leftrightarrow - 3 > x > - 5,5$

Mà x nguyên nên $x \in \{ - 4; - 5\} $

Vậy có 2 giá trị x thỏa mãn

Đáp án đúng là b

Câu 9

Ta có: $\frac{1}{3}$phút = $\frac{1}{3}$ . 60 = 20 giây

$\frac{{108}}{5}$ giây = 21,6 giây

$20\frac{3}{8}$ giây = 20,375 giây

Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất

Đáp án đúng là b

Câu 10

Để x là số nguyên thì $7 \vdots (n + 2)$ hay $(n + 2) \in $ Ư (7) = {1; -1; 7; -7}

Ta có bảng sau:

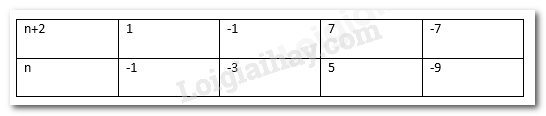
Vậy có 4 giá trị n thỏa mãn điều kiện.

Tổng của các giá trị n đó là: (-1) + (-3) + 5 + (-9) = -8

Đáp án đúng là d

Câu 11

Vì số hữu tỉ $0$ không là số dương cũng không là số âm nên để $y = \dfrac{{2a - 1}}{{ - 3}}$ không dương cũng không âm thì

$y = 0$ suy ra $\dfrac{{2a - 1}}{{ - 3}} = 0$ nên $2a - 1 = 0 $ do đó $a = \dfrac{1}{2}$ .

Đáp án đúng là b

Câu 12

Vì số hữu tỉ $0$ không là số dương cũng không là số âm nên để $y = \dfrac{{4a - 8}}{{ - 2021}}$ không dương cũng không âm thì

$y = 0$ suy ra $\dfrac{{4a - 8}}{{ - 2021}} = 0$ $ \Rightarrow 4a - 8 = 0 \Rightarrow a = 2$ .

Đáp án đúng là b

Câu 13

Để $x = \dfrac{{a - 3}}{2}$ là số nguyên dương thì $\left( {a - 3} \right) > 0$ và $\left( {a - 3} \right) \vdots 2$

Giả sử $a - 3 = 2k\,\left( {k \in {\mathbb{N}^*}} \right)$ suy ra $a = 3 + 2k\,\left( {k \in {\mathbb{N}^*}} \right)$

Đáp án đúng là d

Câu 14

Để $x = \dfrac{{a - 5}}{7}$ là số nguyên dương thì $\left( {a - 5} \right) > 0$ và $\left( {a - 5} \right) \vdots 7$

Giả sử $a - 5 = 7k\,\left( {k \in {\mathbb{N}^*}} \right)$ suy ra $a = 5 + 7k\,\left( {k \in {\mathbb{N}^*}} \right)$

Đáp án đúng là b

Câu 15

$\dfrac{{14}}{{18}} = \dfrac{7}{9}\,;\,\dfrac{{24}}{{26}} = \dfrac{{12}}{{13}}\,\,;\,\dfrac{{72}}{{78}} = \dfrac{{12}}{{13}}.$

Ta có $\dfrac{{26}}{{ - 28}} < 0 < \dfrac{{12}}{{13}};\,\dfrac{{ - 28}}{{30}} < 0 < \dfrac{{12}}{{13}}$ ; $\dfrac{7}{9} = \dfrac{{91}}{{117}} < \dfrac{{108}}{{117}} = \dfrac{{12}}{{13}}$

Vậy có 2 phân số bằng phân số $\dfrac{{12}}{{13}}$ là: $\dfrac{{24}}{{26}}\,;\,\dfrac{{72}}{{78}}.$

Đáp án đúng là b

Câu 16

Ta có:

$\frac{{ - 15}}{{39}} = \frac{{ - 5}}{{13}}$; $\frac{{ - 25}}{{65}} = \frac{{ - 5}}{{13}}$.

Mà: $\frac{{ - 7}}{{ - 26}} = \frac{7}{{26}}$ nên các phân số $\frac{{10}}{{26}};\frac{{35}}{{78}};\frac{{ - 7}}{{ - 26}}$ đều là các phân số dương

$\frac{{ - 5}}{{13}}$ là phân số âm

=> Các phân số $\frac{{10}}{{26}};\frac{{35}}{{78}};\frac{{ - 7}}{{ - 26}}$ không bằng $\frac{{ - 5}}{{13}}$

Vậy có 2 phân số bằng phân số $\frac{{ - 5}}{{13}}$ là: $\frac{{ - 15}}{{39}}$; $\frac{{ - 25}}{{65}}$

Đáp án đúng là d

Câu 17

$0,25 = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{ - 25}}{{ - 100}} = \dfrac{1}{4};\dfrac{5}{{20}} = \dfrac{1}{4}.$

Nên $\dfrac{1}{4} = 0,25 = \dfrac{{ - 25}}{{ - 100}} = \dfrac{5}{{20}}$

Do đó các số $\dfrac{1}{4};0,25\,;\,\dfrac{{ - 25}}{{ - 100}}\,;\,\dfrac{5}{{20}}$ được biểu diễn cùng một điểm trên trục số.

Đáp án đúng là a

Câu 18

Ta có: $2,5 = \dfrac{{25}}{{10}} = \dfrac{{25:5}}{{10:5}} = \dfrac{5}{2}$;

$\dfrac{{10}}{4} = \dfrac{{10:2}}{{4:2}} = \dfrac{5}{2}$;

$\dfrac{6}{{20}} = \dfrac{{6:2}}{{20:2}} = \dfrac{3}{{10}};$

$0,3 = \dfrac{3}{{10}}$.

Suy ra $\dfrac{3}{{10}} = \dfrac{6}{{20}} = 0,3$ và $2,5 = \dfrac{{10}}{4}$.

Vậy các số: $\dfrac{3}{{10}}$; $2,5$; $\dfrac{{10}}{4}$; $\dfrac{6}{{20}};0,3$ được biểu diễn bởi hai điểm phân biệt trên cùng một trục số.

Đáp án đúng là d

Câu 19

Ta có $x = \dfrac{{2002}}{{2003}} < \dfrac{{2003}}{{2003}} = 1$ hay $x < 1$

Và $y = \dfrac{{14}}{{13}} > \dfrac{{13}}{{13}} = 1$ hay $y > 1$

Từ đó suy ra $y > 1 > x$ hay $y > x$ .

Đáp án đúng là c

Câu 20

Ta có $x = \dfrac{{2022}}{{2021}} > \dfrac{{2021}}{{2021}} = 1$ hay $x > 1$

Và $y = \dfrac{{15}}{{16}} < \dfrac{{16}}{{16}} = 1$ hay $y < 1$

Từ đó suy ra $x > 1 > y$ hay $x > y$ .

Đáp án đúng là c

Câu 21

Ta có $x = \dfrac{2}{{ - 5}} = \dfrac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \dfrac{{ - 26}}{{65}}$ và $y = \dfrac{{ - 3}}{{13}} = \dfrac{{ - 3.5}}{{13.5}} = \dfrac{{ - 15}}{{65}}$

Mà $ - 26 < - 15 $ suy ra $\dfrac{{ - 26}}{{65}} < \dfrac{{ - 15}}{{65}}$ hay $x < y$ .

Đáp án đúng là b

Câu 22

Ta có: $a = \dfrac{4}{{15}} = \dfrac{{4.7}}{{15.7}} = \dfrac{{28}}{{105}}$;

$b = - \dfrac{{ - 8}}{{21}} = \dfrac{8}{{21}} = \dfrac{{8.5}}{{21.5}} = \dfrac{{40}}{{105}}$

Vì $28 < 40$ nên $\dfrac{{28}}{{105}} < \dfrac{{40}}{{105}}$ hay $a < b$.

Đáp án đúng là b

Câu 23

Phần bù với $1$ của các số $\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}$ lần lượt là $\dfrac{1}{8};\,\dfrac{1}{3};\dfrac{1}{4};\dfrac{1}{{19}};\dfrac{1}{{28}}$

Mà $28 > 19 > 8 > 4 > 3$ nên $\dfrac{1}{{28}} < \dfrac{1}{{19}} < \dfrac{1}{8} < \dfrac{1}{4} < \dfrac{1}{3}$

Suy ra $\dfrac{{27}}{{28}} > \dfrac{{18}}{{19}} > \dfrac{7}{8} > \dfrac{3}{4} > \dfrac{2}{3}$

Số hữu tỉ lớn nhất là: $\dfrac{{27}}{{28}}$

Đáp án đúng là d