Giải 2. Bài 32: Quan hệ đường vuông góc và đường xiên Toán học Lớp 7

Đề bài

Câu 1

Cho ba điểm $A,\,B,\,C$ thẳng hàng, $B$ nằm giữa $A$ và $C$. Trên đường thẳng vuông góc với $AC$ tại $B$ ta lấy điểm $H$. Khi đó

$AH < BH$
$AH < AB$
$AH > BH$
$AH = BH$

Câu 2

Cho $\Delta ABC$ vuông tại $A,M$ là trung điểm của $AC.$ Gọi $D,E$ lần lượt là hình chiếu của $A$ và $C$ xuống đường thẳng $BM.$ So sánh $BD + BE$ và $AB.$

$BD + BE > 2AB$
$BD + BE < 2AB$
$BD + BE = 2AB$
$BD + BE < AB$

Câu 3

Cho $\Delta ABC$ có $CE$ và $BD$ là hai đường cao. So sánh $BD + CE$ và $AB + AC$ ?

$BD + CE < AB + AC$
$BD + CE > AB + AC$
$BD + CE \le AB + AC$
$BD + CE \ge AB + AC$

Câu 4

Cho $\Delta ABC$ vuông tại $A.$ Trên cạnh $AB$ và $AC$ lấy tương ứng hai điểm $D$ và $E$ ($D,E$ không trùng với các đỉnh của $\Delta ABC$). Chọn đáp án đúng nhất.

$DE > BE > BC$
$DE < BE < BC$
$DE > BE = BC$
$DE < BE = BC$

Câu 5

Cho $\Delta ABC$ có $\widehat C = {90^0}$, $AC < BC$ , kẻ $CH \bot AB$. Trên các cạnh $AB$ và $AC$ lấy tương ứng hai điểm $M$ và $N$ sao cho $BM = BC,CN = CH$. Chọn câu đúng nhất.

$MN \bot AC$
$AC + BC < AB + CH.$
Cả A, B đều sai
Cả A, B đều đúng

Câu 6

Cho góc $\widehat {xOy} = {60^0},$ $A$ là điểm trên tia $Ox,\,B$ là điểm trên tia $Oy$ $(A,B$ không trùng với $O).$

Chọn câu đúng nhất.

$OA + OB \le 2AB$
$OA + OB = 2AB$ khi $OA = OB.$
$OA + OB \ge 2AB$
Cả A, B đều đúng.

Câu 7

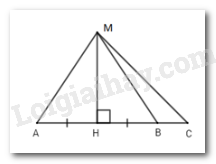
Em hãy chọn đáp án sai trong các đáp án sau:

$MA > MH$
$HB < HC$
$MA = MB$
$MC < MA.$

Đáp án

Câu 1

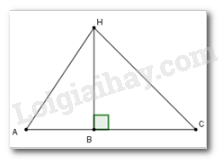
Vì $BH$ là đường vuông góc và $AH$ là đường xiên nên $AH > BH.$

Đáp án đúng là c

Câu 2

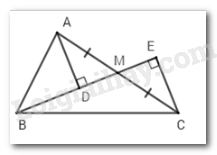
Vì $\Delta ABM$ vuông tại $A$ (gt) nên $BA < BM$ (quan hệ giữa đường vuông góc và đường xiên).

Mà $BM = BD + DM \Rightarrow BA < BD + DM\left( 1 \right)$ .

Mặt khác, $BM = BE - ME \Rightarrow BA < BE - ME\left( 2 \right)$

Cộng hai vế của $\left( 1 \right)$và $\left( 2 \right)$ ta được: $2BA < BD + BE + MD - ME\left( 3 \right)$

Vì $M$ là trung điểm của $AC$ (gt) $ \Rightarrow AM = MC$ (tính chất trung điểm)

Xét tam giác vuông $ADM$ và tam giác vuông $CEM$ có:

$AM = MC\left( {cmt} \right)$

$\widehat {AMD} = \widehat {EMC}$ (đối đỉnh)

$ \Rightarrow \Delta ADM = \Delta CEM$ (cạnh huyền – góc nhọn)

$ \Rightarrow MD = ME\left( 4 \right)$ (2 cạnh tương ứng)

Từ $\left( 3 \right)$và $\left( 4 \right) \Rightarrow BD + BE > 2AB$

Đáp án đúng là a

Câu 3

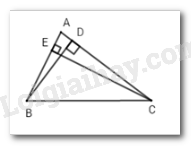
Vì $\left\{ \begin{array}{l}BD \bot AC\left( {gt} \right)\\EC \bot AB\left( {gt} \right)\end{array} \right. \Rightarrow $$BD$ và $CE$ là lần lượt là hai đường vuông góc của hai đường xiên $AC$ và $AB.$

$ \Rightarrow \left\{ \begin{array}{l}BD < AB\\EC < AC\end{array} \right.$ (đường vuông góc nhỏ hơn đường xiên)

$ \Rightarrow BD + EC < AB + AC$

Đáp án đúng là a

Câu 4

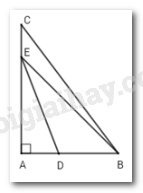
Ta có: Góc EDB là góc ngoài tại đỉnh D của tam giác ADE nên $\widehat {EDB} > \widehat {DAE} = 90^\circ \Rightarrow \widehat {EDB}$ là góc tù.

Góc BEC là góc ngoài tại đỉnh E của tam giác ABE nên $\widehat {BEC} > \widehat {BAE}$( định lí) $ \Rightarrow \widehat {BEC}$ là góc tù.

Xét tam giác BDE có góc BDE là góc tù nên là góc lớn nhất trong tam giác. Cạnh EB đối diện với góc BDE nên là cạnh lớn nhất trong tam giác. Ta được DE < EB.(1)

Xét tam giác BEC có góc BEC là góc tù nên là góc lớn nhất trong tam giác. Cạnh CB đối diện với góc BEC nên là cạnh lớn nhất trong tam giác. Ta được EB < CB.(2)

Từ (1) và (2) $ \Rightarrow $ DE< EB < CB.

Đáp án đúng là b

Câu 5

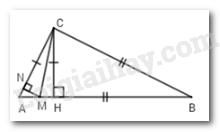
Ta có: $BM = BC\left( {gt} \right) \Rightarrow \Delta BMC$ cân tại $B$ (dấu hiệu nhận biết tam giác cân)

$ \Rightarrow \widehat {MCB} = \widehat {CMB}\left( 1 \right)$ (tính chất tam giác cân)

Lại có: $\left\{ \begin{array}{l}\widehat {BCM} + \widehat {MCA} = \widehat {ACB} = {90^0}\left( {gt} \right)\\\widehat {CMH} + \widehat {MCH} = {90^0}\left( {gt} \right)\end{array} \right.\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right) \Rightarrow \widehat {MCH} = \widehat {MCN}$

Xét $\Delta MHC$ và $\Delta MNC$ có:

$MC$ chung

$\widehat {MCH} = \widehat {MCN}\left( {cmt} \right)$

$NC = HC\left( {gt} \right)$

$ \Rightarrow \Delta MHC = \Delta MNC\left( {c - g - c} \right) \Rightarrow \widehat {MNC} = \widehat {MHC} = {90^0}$ (2 góc tương ứng)

$ \Rightarrow MN \bot AC$ nên A đúng.

Xét $\Delta AMN$ có $AN$ là đường vuông góc hạ từ $A$ xuống $MN$ và $AM$ là đường xiên nên suy ra $AM > AN$ (quan hệ đường vuông góc và đường xiên)

Ta có: $\left\{ \begin{array}{l}BM = BC\left( {gt} \right)\\HC = CN\left( {gt} \right)\\AM > AN\left( {cmt} \right)\end{array} \right.$$ \Rightarrow BM + MA + HC > BC + CN + NA$$ \Leftrightarrow AB + HC > BC + AC$

Đáp án đúng là d

Câu 6

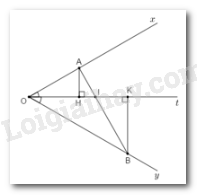
Kẻ tia phân giác $Ot$ của $\widehat {xOy}$ nên $\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.$

Gọi $I$ là giao của $Ot$ và $AB$. Kẻ $AH \bot Ot, BK \bot Ot$

Xét $\Delta OAH$ có $\widehat {AOH} = {30^o}$ nên $OA = 2AH.$

Vì $AH,\,AI$ lần lượt là đường vuông góc, đường xiên kẻ từ $A$ đến $Ot$ nên $AH \le AI$ do đó $OA \le 2AI$ (1)

Xét $\Delta OBK$ có $\widehat {BOK} = {30^o}$ nên $OB = 2BK.$

Vì $BK,\,BI$ lần lượt là đường vuông góc, đường xiên kẻ từ $B$ đến $Ot$ nên $BK \le BI$ do đó $OB \le 2BI$ (2)

Cộng (1) với (2) theo vế với vế ta được:

$OA + OB \le 2AI + 2BI = 2\left( {AI + BI} \right) = 2AB$

Dấu “=” xảy ra khi và chỉ khi $H,\,I,K$ trùng nhau hay $AB \bot Ot$ suy ra $\widehat {AIO} = \widehat {BIO} = {90^o}.$

Xét $\Delta OAI$ và $\Delta OBI$ có:

$\widehat {AIO} = \widehat {BIO} = {90^o}$

$\widehat {AOI} = \widehat {BOI}$ (vì $Ot$ là phân giác của $\widehat {xOy}$)

$OI$ cạnh chung

$ \Rightarrow \Delta OAI = \Delta OBI$ (g.c.g)

$ \Rightarrow OA = OB$ (hai cạnh tương ứng).

Vậy $OA + OB = 2AB$ khi $OA = OB.$

Đáp án đúng là d