Giải 5. Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Toán học Lớp 7

Đề bài

Câu 1

Để hai tam giác cân bằng nhau thì phải cần điều kiện là:

Có các cặp cạnh đáy bằng nhau
Có hai cặp cạnh bên bằng nhau
Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau
Có một cặp góc ở đáy bằng nhau.

Câu 2

Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:

$\widehat B = \widehat C$
$\widehat C = \frac{{{{180}^0} - \widehat A}}{2}$
$\widehat A = {180^0} - 2\widehat C$
$\widehat B \ne \widehat C$

Câu 3

Một tam giác cân có góc ở đỉnh bằng ${54^0}$ thì số đo góc ở đáy là:

${54^0}$
${63^0}$
${72^0}$
${90^0}$

Câu 4

Phát biểu nào sau đây là đúng:

Góc ở đỉnh của một tam giác cân thì nhỏ hơn ${90^0}$
Trong một tam giác bất kì góc lớn nhất là góc tù
Trong một tam giác vuông có thể có một góc tù
Góc ở đáy của một tam giác cân không thể là góc tù.

Câu 5

Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.

IH = IK
IH = IL
IH +IK = IL
IK = IL

Câu 6

Cho tam giác ABC cân tại đỉnh A với $\widehat A = {80^0}$. Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?

DE // BC
$\widehat B = {50^0}$
$\widehat {ADE} = {50^0}$
Cả ba phát biểu trên đều sai

Câu 7

Cho tam giác ABC có $\widehat A = {60^ \circ }$. Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.

Khẳng định đúng là:

BN = CM
BM = CN
$\widehat {MAN} = 120^\circ $
$\Delta MBN = \Delta NCM$

Câu 8

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất

Tam giác AMB đều
AM = BM = CM
AM = BC
AB + AC = BC

Câu 9

Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.

Hình chữ nhật
Hình vuông
Hình thoi
Hình bình hành

Câu 10

Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính $\widehat {MAN}$.

30$^\circ $
45$^\circ $
67,5$^\circ $
60$^\circ $

Câu 11

Chọn câu sai.

Tam giác đều có ba góc bằng nhau và bằng $60^\circ .$
Tam giác đều có ba cạnh bằng nhau.
Tam giác cân là tam giác đều.
Tam giác đều là tam giác cân.

Câu 12

Hai góc nhọn của tam giác vuông cân bằng nhau và bằng

Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau.
Tam giác cân có ba cạnh bằng nhau.
Tam giác vuông cân là tam giác đều.
Tam giác đều có ba góc bằng nhau và bằng ${45^o}.$

Câu 13

Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:

$30^\circ $
$45^\circ $
$60^\circ $
$90^\circ $

Câu 14

Một tam giác cân có góc ở đỉnh bằng ${64^0}$ thì số đo góc ở đáy là:

Tam giác cân
Tam giác vuông cân
Tam giác vuông
Tam giác đều

Câu 15

Một tam giác cân có góc ở đáy bằng ${70^0}$ thì số đo góc ở đỉnh là:

$\widehat B = \widehat C$
$\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}$
$\widehat A = {180^0} - 2\widehat C$
$\widehat B \ne \widehat C$

Câu 16

Số tam giác cân trong hình vẽ dưới đây là:

$\widehat B = {90^o} + \alpha $
$\widehat B = \dfrac{{{{180}^0} - \alpha }}{2}$
$\widehat B = {180^0} - 2\alpha $
$\widehat B = {90^o} - \alpha $

Câu 17

Tính số đo $x$ trên hình vẽ sau:

${54^0}$
${58^0}$
${72^0}$
${90^0}$

Câu 18

Cho tam giác $ABC$ vuông cân ở $A.$ Trên đáy $BC$ lấy hai điểm $M,N$ sao cho $BM = CN = AB.$

${76^0}$
${67^0}$
${88^0}$
${60^0}$

Câu 19

Cho tam giác $ABC$ cân tại đỉnh $A$ với $\widehat A = {80^0}$. Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?

${54^0}$
${63^0}$
${70^0}$
${40^0}$

Câu 20

Cho tam giác $ABC$ có $\widehat A = 90^\circ ;\,AB = AC$. Khi đó

${46^0}$
${64^0}$
${67^0}$
${76^0}$

Câu 21

Cho tam giác $ABC$ có $M$ là trung điểm của $BC$ và $AM = \dfrac{{BC}}{2}$. Số đo góc $BAC$ là

$2$
$1$
$3$
$4$

Câu 22

Tam giác $ABC$ có $\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .$ Trên tia đối của tia $AC$ lấy điểm $E$ sao cho $AE = AB.$ Tính số đo góc $CBE.$

$1$ tam giác đều và 2 tam giác cân
2 tam giác cân
3 tam giác đều
$1$ tam giác đều và 3 tam giác cân

Câu 23

Cho tam giác $ABC$ có $\widehat A = 120^\circ .$ Trên tia phân giác của góc $A$ lấy điểm $D$ sao cho $AD = AB + AC.$ Khi đó tam giác $BCD$ là tam giác gì?

$x = 45^\circ .$
$x = 40^\circ .$
$x = 35^\circ .$
$x = 70^\circ .$

Câu 24

Cho tam giác $ABC$ có $\widehat A = {60^ \circ }$. Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$

$x = {33^o}$
$x = {32^o}$
$x = {32^o}30'$
$x = 30^\circ $

Đáp án

Câu 1

Để hai tam giác cân bằng nhau thì phải cần điều kiện là: Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau.

Khi đó hai tam giác cân bằng nhau theo trường hợp góc – cạnh – góc.

Đáp án đúng là c

Câu 2

Do tam giác ABC cân nên $\widehat B = \widehat C$

Xét tam giác ABC ta có: $\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \frac{{{{180}^0} - \widehat A}}{2}$ hay $\widehat A = {180^0} - 2\widehat C$

Đáp án đúng là d

Câu 3

Do tam giác ABC cân nên $\widehat B = \widehat C$

Đáp án đúng là b

Câu 4

Giả sử xét trong tam giác ABC cân tại A.

Vì $180^\circ - \widehat A < 180^\circ \Rightarrow \frac{{180^\circ - \widehat A}}{2} < \frac{{180^\circ }}{2} = 90^\circ $

Vậy góc ở đáy của một tam giác cân không thể là góc tù.

Đáp án đúng là d

Câu 5

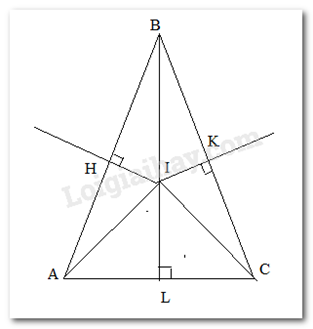
Vì tam giác ABC cân tại B nên BA = BC

Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK

Xét tam giác vuộng BHI và BKI có:

BI chung

BH = BK

$ \Rightarrow BHI = \Delta BKI$ ( cạnh huyền – cạnh góc vuông)

$ \Rightarrow $ IH = IK (hai cạnh tương ứng).

Đáp án đúng là a

Câu 6

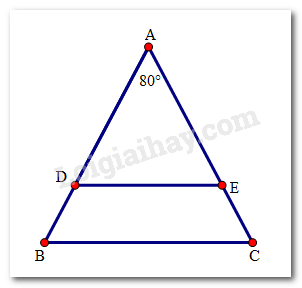
Do tam giác ABC cân tại A nên $\widehat B = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{80}^0}}}{2} = {50^0}$

Ta thấy tam giác ADE cân do AD = AE

$ \Rightarrow \widehat {ADE} = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{80}^0}}}{2} = {50^0}$

Do đó $\widehat B = \widehat {ADE}$ .

Mà hai góc này ở vị trí đồng vị nên ED // BC ( Dấu hiệu nhận biết 2 đường thẳng song song)

Vậy D là đáp án sai.

Đáp án đúng là d

Câu 7

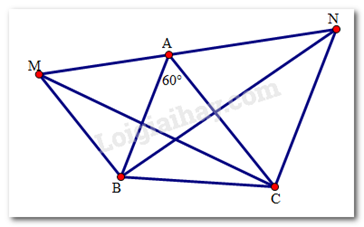
Ta có:

$\begin{array}{l}\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\end{array}$

$ \Rightarrow $$\widehat {MAC} = \widehat {BAN}$ .

Xét hai tam giác ABN và AMC có:

AM = AB (do tam giác AMB đều)

$\widehat {MAC} = \widehat {BAN}$ (cmt)

AN = AC (do tam giác ANC đều)

Do đó $\Delta ABN = \Delta AMC(c.g.c)$

$ \Rightarrow $BN = CM (hai cạnh tương ứng).

Đáp án đúng là a

Câu 8

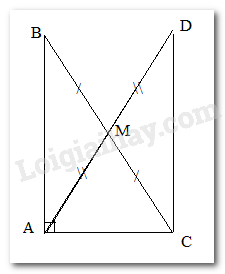
Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Khi đó, 2. AM = AD

Xét tam giác ABM và DCM, có:

AM = DM

$\widehat {AMB} = \widehat {CMD}$ ( đối đỉnh)

BM = CM ( gt)

$ \Rightarrow \Delta ABM = \Delta DCM$ ( c.g.c)

$ \Rightarrow \widehat {ABC} = \widehat {BCD}$ (2 góc tương ứng); AB = CD ( 2 cạnh tương ứng)

Mà 2 góc ABC và BCD ở vị trí so le trong

$ \Rightarrow $AB // CD

Mà AB $ \bot $ AC

$ \Rightarrow $ CD $ \bot $ AC ( tính chất)

Xét tam giác vuông ABC và CDA có:

AC chung

$\widehat {BAC} = \widehat {DCA}( = 90^\circ )$

AB = CD( cmt)

$ \Rightarrow \Delta ABC = \Delta CDA$ ( c.g.c)

$ \Rightarrow $ AD = BC ( 2 cạnh tương ứng)

$ \Rightarrow $ 2. AM = BC

$ \Rightarrow $ AM = MB = MC

Đáp án đúng là b

Câu 9

Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)

Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)

Xét tam giác AOM và AON có:

OM = ON

$\widehat {AOM} = \widehat {AON}( = 90^\circ )$

AO chung

$ \Rightarrow \Delta AOM = \Delta AON$ ( c.g.c)

$ \Rightarrow $ AM = AN ( 2 cạnh tương ứng)

Mà MA = MB; NA = NB

$ \Rightarrow $ MA = MB = NB = NA

$ \Rightarrow $ Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)

Đáp án đúng là c

Câu 10

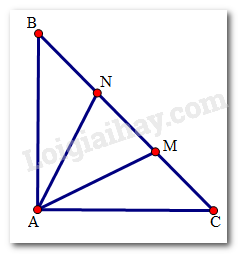
Do tam giác ABC vuông cân ở A nên $\widehat B = \widehat C = {45^0}$.

Xét tam giác AMB có: BM = BA (gt), nên tam giác AMB cân ở B.

Do đó $\widehat {AMB} = \frac{{{{180}^0} - \widehat B}}{2} = \frac{{{{180}^0} - {{45}^0}}}{2} = 67,5^\circ $

Chứng minh tương tự ta được tam giác ANC cân ở C và $\widehat {ANC} = 67,5^\circ $.

Xét tam giác AMN, ta có:

$\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) = {180^0} - {135^0} = {45^0}$.

Vậy $\widehat {MAN} = {45^0}$

Đáp án đúng là b

Câu 11

Tam giác đều là tam giác có ba cạnh bằng nhau.

Trong tam giác đều, mỗi góc bằng ${60^0}.$

Nên A, B đúng.

Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau.

Vậy C sai.

Đáp án đúng là c

Câu 12

Tam giác đều là tam giác có ba cạnh bằng nhau. Trong tam giác đều, ba góc bằng nhau và cùng bằng ${60^0}$ (A đúng; D sai).

Tam giác cân là tam giác có hai cạnh bằng nhau (B sai).

Tam giác vuông cân là tam giác cân có góc ở đỉnh bằng ${90^o}$ nên tam giác vuông cân không phải tam giác đều (C sai).

Đáp án đúng là a

Câu 13

Mỗi góc nhọn của tam giác vuông cân bằng ${45^0}.$

Đáp án đúng là b

Câu 14

Áp dụng định lí tổng các góc của một tam giác vào $\Delta ABC$, ta có:

$\widehat A + \widehat B + \widehat C = {180^o}$

$ \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}$

$\Delta ABC$ có $\widehat A = {90^o};\,\widehat B = \widehat C = {45^o}$ nên $\Delta ABC$ là tam giác vuông cân.

Đáp án đúng là b

Câu 15

Do tam giác ABC cân nên $\widehat B = \widehat C$

Xét tam giác ABC ta có: $\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}$ hay $\widehat A = {180^0} - 2\widehat C$

Đáp án đúng là d

Câu 16

Do tam giác ABC cân tại $A$ nên $\widehat B = \widehat C$.

Áp dụng định lí tổng các góc của một tam giác vào $\Delta ABC$, ta có:

$\widehat A + \widehat B + \widehat C = {180^0}$

$ \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A$

$ \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - 2\alpha }}{2} = {90^o} - \alpha $.

Đáp án đúng là d

Câu 17

Sử dụng cách tính số đo các góc trong tam giác $ABC$ cân tại $A.$

Góc ở đỉnh $\widehat A = {180^0} - 2\widehat C$ và góc ở đáy $\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}.$

Áp dụng ta có số đo góc ở đáy bằng: $\dfrac{{{{180}^0} - {{64}^0}}}{2} = {58^0}$

Đáp án đúng là b

Câu 18

Sử dụng cách tính số đo góc ở đáy của tam giác cân ta có:

Số đo góc ở đáy bằng: $\dfrac{{{{180}^0} - {{46}^0}}}{2} = {67^0}.$

Đáp án đúng là b

Câu 19

Tổng số đo hai góc ở đáy là $70^o.2 = 140^\circ $

Vì tổng ba góc của tam giác bằng $180^\circ $ nên số đo góc ở đỉnh tam giác cân này là

$180^\circ - 140^\circ = 40^\circ .$

Đáp án đúng là d

Câu 20

Tổng số đo hai góc ở đáy là: ${52^o}.2 = 104^\circ $

Vì tổng ba góc của tam giác bằng $180^\circ $ nên số đo góc ở đỉnh tam giác cân là:

$180^\circ - 104^\circ = 76^\circ .$

Đáp án đúng là d

Câu 21

Từ hình vẽ ta có $AB = AE;BC = DE$

Vì $AB = AE \Rightarrow \Delta ABE$ cân tại $A.$

Suy ra $\widehat B = \widehat E$ (hai góc ở đáy)

Xét tam giác $ABC$ và $AED$ có: $AB = AE;\widehat B = \widehat E\left( {cmt} \right);BC = DE$ nên $\Delta ABC = \Delta AED\left( {c - g - c} \right)$

Do đó $AC = AD$ (hai cạnh tương ứng) suy ra $\Delta ACD$ cân tại $A.$

Vậy có hai tam giác cân trên hình vẽ.

Đáp án đúng là a

Câu 22

Từ hình vẽ ta có: $DC = CE = ED = EB = CA$.

Vì $DC = CE = ED$ nên $\Delta CDE$ là tam giác đều.

Vì $DC = CA$ nên $\Delta ACD$ cân tại $C.$

Vì $ED = EB$ nên $\Delta BED$ cân tại $E.$

$\Delta CDE$ là tam giác đều nên $\widehat {DCE} = \widehat {DEC} = {60^o}$.

Ta có: $CA = EB$

$ \Rightarrow CA + CE = EB + CE$

$ \Rightarrow AE = BC$

Xét $\Delta ADE$ và $\Delta BDC$ có:

$DE = DC\,(gt)$

$AE = BC\,(cmt)$

$\widehat {DEA} = \widehat {DCB} = {60^o}$

$ \Rightarrow \Delta ADE = \Delta BDC\,(c.g.c)$

$ \Rightarrow DA = DB$ (hai cạnh tương ứng).

$\Delta ADB$ có $DA = DB$ (cmt) nên $\Delta ADB$ cân tại $D$.

Vậy hình vẽ có 1 tam giác đều và 3 tam giác cân.

Đáp án đúng là d

Câu 23

Tam giác $ABC$ cân tại $A$ (vì $AB = AC$ ) có $\widehat A = 40^\circ $ nên $\widehat B = \widehat {ACB} = \dfrac{{180^\circ - 40^\circ }}{2} = 70^\circ $

Mà $\widehat {ACB}$ là góc ngoài của tam giác $ACD$ nên $\widehat {ACB} = \widehat {CAD} + \widehat {CDA}$

Lại có $\Delta CAD$ cân tại $C \Rightarrow \widehat {CAD} = \widehat {CDA} = x$ (tính chất)

Nên $\widehat {ACB} = \widehat {CAD} + \widehat {CDA} = 2x \Rightarrow x = \dfrac{{\widehat {ACB}}}{2}$$ = \dfrac{{70^\circ }}{2} = 35^\circ .$

Vậy $x = 35^\circ .$

Đáp án đúng là c