1. Trang chủ
  2. Lớp 7
  3. Toán học Lớp 7
  4. Bài tập trắc nghiệm Toán Lớp 7 Kết nối tri thức
  5. Chương 4: Tam giác bằng nhau Kết nối tri thức
  6. 2. Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Đề bài

Câu 1

Cho \(\Delta\)ABC có AB = AC và  MB = MC (\(M \in BC\)).Chọn câu sai.

  1. \(\Delta AMC = \Delta BCM\)

  2. \(AM \bot BC\)

  3. \(\widehat {BAM} = \widehat {CAM}\)     

  4. \(\Delta AMB = \Delta AMC\)

Câu 2

Cho tam giác \(MNP\)  có MN = MP. Gọi \(A\) là trung điểm của \(NP.\) Biết \(\widehat {NMA} = {20^0}\) thì số đo góc \(MPN\) là:

  1. 50\(^\circ \)

  2. 40\(^\circ \)

  3. 70\(^\circ \)

  4. 80\(^\circ \)

Câu 3

Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)

  1. \(\widehat A = \widehat D = 65^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)

  2. \(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 65^\circ .\) 

  3. \(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\) 

  4. \(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 75^\circ .\)

Câu 4

Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt ở A và B. Vẽ các cung tròn tâm A và tâm B có bán kính 3cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính \(\widehat {xOC}\) .

  1. \({40^0}\)

  2. \({25^0}\)

  3. \({80^0}\)

  4. \({90^0}\)

Câu 5

Cho hình vẽ sau:

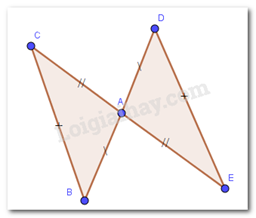
Khẳng định đúng là:

  1. \(\Delta ABC = \Delta DEA\)

  2. \(\widehat D = \widehat A\)

  3. \(\widehat E = \widehat B\)

  4. \(\widehat C = \widehat E\)

Câu 6

Cho tam giác \(ABC\)  có \(AB < AC\) . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi \(O\)  là một điểm nằm ở trong tam giác sao cho \(OA = OC,OB = OE.\) Khi đó:

  1. \(\Delta AOB = \Delta CEO\)

  2. \(\Delta AOB = \Delta COE\)

  3. \(\widehat {AOB} = \widehat {OEC}\)       

  4. \(\widehat {ABO} = \widehat {OCE}\)

Câu 7

Cho hình vẽ sau. Tam giác bằng với tam giác DEA là:

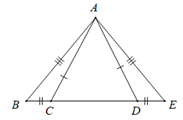
  1. Tam giác ABC

  2. Tam giác CBA

  3. Tam giác DBA

  4. Tam giác BCA

Câu 8

Cho hình dưới đây.

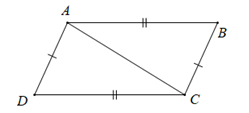
Chọn câu sai.

  1. \(AD//BC\)

  2. \(AB//CD\)

  3. \(\Delta ABC = \Delta CDA\)

  4. \(\Delta ABC = \Delta ADC\)

Câu 9

Cho \(\Delta ABC = \Delta MNP.\) Biết AC = 6 cm, NP = 8 cm và chu vi của tam giác MNP bằng 22cm. Tìm khẳng định sai:

  1. MP = 8 cm

  2. BC = 8 cm

  3. MN = 8 cm

  4. AB = 8 cm

Câu 10

Cho \(\Delta ABC = \Delta DEF.\) Cho \(\widehat E = 46^\circ \). Khẳng định đúng là:

  1. \(\widehat A = 46^\circ \)

  2. \(\widehat B = 46^\circ \)

  3. \(\widehat F = 46^\circ \)

  4. \(\widehat C = 46^\circ \)

Câu 11

Cho \(\Delta ABC = \Delta MNP.\) Chọn câu sai.

  1. \(AB = MN\) 

  2. $AC = NP$   

  3. \(\widehat A = \widehat M\) 

  4. \(\widehat P = \widehat C\)

Câu 12

Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A = {33^0}\).  Khi đó

  1. \(PQ = DE\)

  2. \(PR = EF\)

  3. \(\widehat Q = \widehat E\)

  4. \(\widehat D = \widehat P\)

Câu 13

Cho hai tam giác \(ABC\) và \(DEF\) có \(AB = EF;\,BC = FD;AC = ED;\) \(\widehat A = \widehat E;\widehat B = \widehat F;\widehat D = \widehat C\). Khi đó

  1. \(\widehat D = 33^\circ \) 

  2. \(\widehat D = 42^\circ \)   

  3. \(\widehat E = 32^\circ \) 

  4. \(\widehat D = 66^\circ \)

Câu 14

Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A = {32^0},\widehat F = {78^0}\). Tính \(\widehat B;\widehat E.\)

  1. \(\widehat C = {45^0}\)

  2. \(\widehat B = {45^0}\)

  3. \(\widehat A = {45^0}\)

  4. \(\widehat C = {90^0}\)

Câu 15

Cho \(\Delta ABC = \Delta MNP.\) Biết \(AB = 5cm,\) \(MP = 7cm\) và chu vi của tam giác $ABC$ bằng $22cm.$ Tính các cạnh còn lại của mỗi tam giác.

  1. \(\Delta ABC = \Delta DEF\) 

  2. \(\Delta ABC = \Delta EFD\)   

  3. \(\Delta ABC = \Delta FDE\) 

  4. \(\Delta ABC = \Delta DFE\)

Câu 16

Cho \(\Delta ABC = \Delta DEF.\) Biết rằng \(AB = 6cm,\) \(AC = 8cm\) và \(EF = 10cm.\) Chu vi tam giác \(DEF\) là

  1. \(\Delta MNP = \Delta IJK\)

  2. \(\Delta MNP = \Delta IKJ\)

  3. \(\Delta MNP = \Delta KIJ\)

  4. \(\Delta MNP = \Delta JKI\)

Câu 17

Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)

  1. \(\widehat B = \widehat E = 60^\circ .\) 

  2. $\widehat B = 60^\circ ;\widehat E = 70^\circ .$   

  3. \(\widehat B = \widehat E = 78^\circ .\) 

  4. \(\widehat B = \widehat E = 70^\circ .\)

Câu 18

Cho \(\Delta DEF = \Delta MNP.\) Biết \(EF + FD = 10cm,\) \(NP - MP = 2cm,\) \(DE = 3cm.\) Tính độ dài cạnh \(FD.\)

  1. \(\widehat D = {80^0};\,\widehat K = {40^0}\)

  2. \(\widehat D = {40^0};\,\widehat K = {60^0}\)

  3. \(\widehat D = {60^0};\,\widehat K = {80^0}\)

  4. \(\widehat D = {40^0};\,\widehat K = {80^0}\)

Câu 19

Cho tam giác $ABC$ (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là $O,H,K.$ Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng: \(\widehat A = \widehat O,\widehat B = \widehat K.\)

  1. \(NP = BC = 9\,cm.\) 

  2. \(NP = BC = 11\,cm.\)   

  3. \(NP = BC = 10\,cm.\) 

  4. \(NP = 9cm;\,BC = 10\,cm.\)

Câu 20

Cho \(\Delta ABC = \Delta MNP\) trong đó \(\widehat A = 30^\circ ;\widehat P = 60^\circ .\) So sánh các góc \(N;\,M;\,P.\)  

  1. \(MN = 7\,cm;\,AC = 7\,cm;\,BC = NP = 10cm\)

  2. \(MN = AC = 10\,\,cm;\,BC = NP = 7cm\)

  3. \(MN = 7\,cm;\,AC = 10\,\,cm;\,BC = NP = 7cm\)

  4. \(MN = 10\,cm;\,AC = 7\,cm;\,BC = NP = 7cm\)

Câu 21

Cho hai tam giác $ABD$  và $CDB$  có cạnh chung $BD.$  Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai:

  1. \(24\,cm\) 

  2. \(20\,cm\)   

  3. \(18\,cm\) 

  4. \(30\,cm\)

Câu 22

Cho tam giác $ABD$ và tam giác $IKH$ có $AB = KI,AD = KH,DB = IH.$

  1. \(30\,cm\)

  2. \(22\,cm\)

  3. \(18\,cm\)

  4. \(20\,cm\)

Câu 23

Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$  vẽ tam giác $ABC$  sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$  sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.

  1. \(\widehat A = \widehat D = 65^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\) 

  2. \(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 65^\circ .\)   

  3. \(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\) 

  4. \(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 75^\circ .\)

Câu 24

Trên đường thẳng \(xy\) lấy hai điểm \(A,B\). Trên cùng nửa mặt phẳng bờ \(xy\)  lấy hai điểm \(C\) và \(C'\) sao cho \(AC = BC';BC = AC'.\)

  1. \(\widehat A = \widehat D = {105^0};\,\widehat C\, = \widehat F = {40^0}.\)

  2. \(\widehat A = \widehat D = {90^0};\,\widehat C\, = \widehat F = {50^0}.\)

  3. \(\widehat A = \widehat D = {95^0};\,\widehat C\, = \widehat F = {40^0}.\)

  4. \(\widehat A = \widehat D = {40^0};\,\widehat C\, = \widehat F = {95^0}.\)

Đáp án

Câu 1

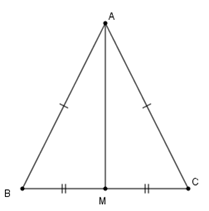
Xét \(\Delta AMB\) và \(\Delta AMC\) có

\(AB = AC\,\left( {gt} \right)\)

\(MB = MC\left( {gt} \right)\)

Cạnh \(AM\) chung

Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)

Suy ra \(\widehat {BAM} = \widehat {CAM}\) và \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng bằng nhau)

Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \)  (hai góc kề bù)

Nên \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ .\) Hay \(AM \bot BC.\)

Vậy B, C, D đúng, A sai.

Đáp án đúng là a

Câu 2

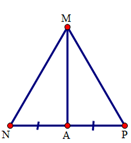
Xét tam giác \(NAM\)  và tam giác \(PAM\) có:

\(MN = MP,\) \(NA = PA,\) \(MA\)  là cạnh chung.

Do đó \(\Delta NAM = \Delta PAM\,\left( {c - c - c} \right).\)

Nên \(\widehat {ANM} = \widehat {APM}\) ; \(\widehat {NMA} = \widehat {PMA}\) (hai góc tương ứng)

Do đó \(\widehat {NMP} = \widehat {NMA} + \widehat {PMA} = 20^\circ  + 20^\circ  = 40^\circ \)

Áp dụng định lý tổng 3 góc trong tam giác \(MNP\) có:

\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0} \\ 2\widehat {MPN} + \widehat {NMP} = {180^0}\)

Suy ra \(\widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)

Đáp án đúng là c

Câu 3

Vì \(\Delta ABC = \Delta DEF\) nên \(\widehat A = \widehat D;\,\widehat B = \widehat E = 55^\circ ;\widehat C\, = \widehat F.\) ( các góc tương ứng)

Xét tam giác \(ABC\) có \(\widehat A + \widehat B = 130^\circ  \Rightarrow \widehat A = 130^\circ  - \widehat B\) \( = 130^\circ  - 55^\circ  = 75^\circ \)

Lại có \(\widehat A + \widehat B + \widehat C = 180^\circ  \Rightarrow \widehat C = 180^\circ  - \left( {\widehat A + \widehat B} \right)\) \( = 180^\circ  - 130^\circ  = 50^\circ .\)

Vậy \(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)

Đáp án đúng là c

Câu 4

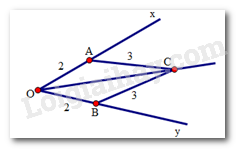
Xét hai tam giác OAC và OBC có:

OA = OB (= 2cm)

OC chung

AC = BC (= 3cm)

Nên \(\Delta OAC = \Delta OBC(c.c.c)\)

Do đó \(\widehat {AOC} = \widehat {COB}\) (hai góc tương ứng).

Mà \(\widehat {AOC} + \widehat {COB} = {50^0}\) nên \(\widehat {AOC} = \widehat {COB} = \frac{{{{50}^0}}}{2} = {25^0}\)

Vậy \(\widehat {xOC} = {25^0}\).

Đáp án đúng là b

Câu 5

Xét \(\Delta \)ABC và \(\Delta \)ADE, ta có:

AB = AD

BC = DE

AC = AE

\( \Rightarrow \Delta ABC = \Delta ADE\) ( c.c.c)

\( \Rightarrow \widehat {BAC} = \widehat {DAE};\widehat B = \widehat D;\widehat C = \widehat E\) ( các góc tương ứng)

Đáp án đúng là d

Câu 6

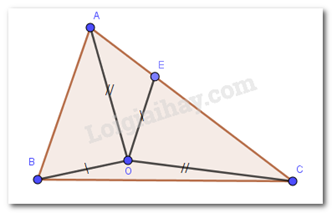
Xét  tam giác \(AOB\) và tam giác \(COE\)  có:

\(AB = CE\left( {gt} \right);AO = CO;OB = OE\)

Do đó: \(\Delta AOB = \Delta COE(c.c.c)\) suy ra \(\widehat {AOB} = \widehat {COE};\,\widehat {ABO} = \widehat {OEC}\) (hai góc tương ứng bằng nhau)

Nên A, C, D sai, B đúng.

Đáp án đúng là b

Câu 7

Xét tam giác DEA và tam giác CBA, ta có:

DE = CB

EA = BA

DA = CA

\( \Rightarrow \Delta DEA = \Delta CBA\) ( c.c.c)

Đáp án đúng là b

Câu 8

Xét tam giác \(ADC\) và \(CBA\) có

\(AB = CD\)

\(AD = BC\)

\(DB\)  chung

\( \Rightarrow \Delta ADC = CBA\left( {c.c.c} \right)\)

Do đó \(\widehat {DAC} = \widehat {BCA}\) (hai góc tương ứng)

Mà hai góc ở vị trí so le trong nên \(AD//BC.\)

Tương tự ta có \(AB//DC.\)

Vậy A, B, C đúng, D sai.

Đáp án đúng là d

Câu 9

Vì \(\Delta ABC = \Delta MNP.\)

\( \Rightarrow \) AB  = MN, BC = NP; AC = MP

Mà AC = 6 cm, NP = 8 cm

Nên MP = 6 cm, BC = 8 cm

Chu vi của tam giác MNP bằng 22cm nên MN + NP + MP = 22 cm hay MN + 8 + 6 = 22 cm nên MN = 8 cm

Do đó, AB = MN = 8 cm

Vậy các khẳng định B,C,D là đúng; khẳng định A sai.

Đáp án đúng là a

Câu 10

Vì \(\Delta ABC = \Delta DEF.\)

\( \Rightarrow \) ( 2 góc tương ứng)

\( \Rightarrow \widehat B = 46^\circ \)

Đáp án đúng là b

Câu 11

Ta có \(\Delta ABC = \Delta MNP\)\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat M\\\widehat C = \widehat P\\\widehat B = \widehat N\\AB = MN\\AC = MP\\BC = NP\end{array} \right.\)

Nên A, C, D đúng, B sai.

Đáp án đúng là b

Câu 12

Ta có: \(\Delta PQR = \Delta DEF\) suy ra \(PQ = DE;\) \(PR = DF;\) \(QR = EF;\) \(\widehat P = \widehat D;\) \(\widehat Q = \widehat E;\) \(\widehat R = \widehat F.\)

Do đó A, C, D đúng, B sai.

Đáp án đúng là b

Câu 13

\(\Delta ABC = \Delta DEF\)\( \Rightarrow \widehat D = \widehat A\)  (hai góc tương ứng).

Nên \(\widehat D = 33^\circ .\)

Đáp án đúng là a

Câu 14

Ta có: \(\Delta ABC = \Delta DEF\) \( \Rightarrow \widehat C = \widehat F\) (hai góc tương ứng)

Mà \(\widehat F = {45^0}\)

Do đó \(\widehat C = {45^0}\).

Đáp án đúng là a

Câu 15

Xét tam giác \(ABC\) và \(DEF\) có \(AB = EF;\,BC = FD;AC = ED;\)\(\widehat A = \widehat E;\widehat B = \widehat F;\widehat D = \widehat C\) nên \(\Delta ABC = \Delta EFD\)

Đáp án đúng là b

Câu 16

Xét hai tam giác \(MNP\) và \(IJK\) có: \(MN = IK;\,NP = KJ;MP = JI;\)\(\widehat M = \widehat I;\widehat J = \widehat P;\widehat N = \widehat K\) nên \(\Delta MNP = \Delta IKJ\).

Đáp án đúng là b

Câu 17

Vì \(\Delta ABC = \Delta DEF\) nên \(\widehat D = \widehat A = 32^\circ ;\,\widehat B = \widehat E;\,\widehat C = \widehat F = 78^\circ \) (các góc tương ứng bằng nhau)

Xét tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác)

Suy ra \(\widehat B = 180^\circ  - \widehat A - \widehat C = 180^\circ  - 32^\circ  - 78^\circ \)\( = 70^\circ .\)

Vậy \(\widehat B = \widehat E = 70^\circ .\)

Đáp án đúng là d

Câu 18

Vì \(\Delta IHK = \Delta DEF\) nên \(\widehat D = \widehat I = {40^0};\,\widehat H = \widehat E = {60^0}\) (các góc tương ứng bằng nhau)

Xét tam giác \(IHK\) có: \(\widehat I + \widehat H + \widehat K = {180^0}\) (định lý tổng ba góc của một tam giác)

Suy ra \(\widehat K = {180^0} - \widehat I - \widehat H = {180^0} - {40^0} - {60^0} = {80^0}\)

Vậy \(\widehat D = {40^0};\,\widehat K = {80^0}\).

Đáp án đúng là d

Câu 19

Vì \(\Delta ABC = \Delta MNP\) nên \(AB = MN = 5\,cm;\,AC = MP = 7\,cm;\,BC = NP\) (các cạnh tương ứng bằng nhau)

Chu vi tam giác \(ABC\) là \(AB + BC + AC = 22\,cm \Rightarrow BC = 22 - AB - AC\)\( = 22 - 5 - 7 = 10\,cm.\)

Vậy \(NP = BC = 10\,cm.\)

Đáp án đúng là c

Câu 20

Vì \(\Delta ABC = \Delta MNP\) nên \(AB = MN = 7\,cm;\,AC = MP = 10\,cm;\,BC = NP\) (các cạnh tương ứng bằng nhau)

Chu vi tam giác \(ABC\) là: \(AB + BC + AC = 24 \Rightarrow BC = 24 - AB - AC\) \( = 24 - 7 - 10 = 7\,cm\)

\( \Rightarrow NP = \,BC = 7\,cm\).

Vậy \(MN = 7\,cm;\,AC = 10\,\,cm;\,BC = NP = 7cm\)

Đáp án đúng là c

Câu 21

Vì \(\Delta ABC = \Delta DEF\) nên \(AB = DE = 6cm;\,AC = DF = 8cm;\,BC = EF = 10\,cm\) (các cạnh tương ứng bằng nhau).

Chu vi tam giác \(ABC\) là \(AB + BC + AC = 6 + 10 + 8 = 24\,cm.\)

Chu vi tam giác \(DEF\) là \(DE + DF + EF = 6 + 8 + 10 = 24\,cm.\)

Đáp án đúng là a

Câu 22

Vì \(\Delta ABC = \Delta DEF\) nên \(AB = DE = 5cm;\,AC = DF = 12cm\) (các cạnh tương ứng bằng nhau).

Chu vi tam giác \(DEF\) là: \(DE + DF + EF = 5 + 12 + 13 = 30\,cm.\)

Đáp án đúng là a

Câu 23

Vì \(\Delta ABC = \Delta DEF\) nên \(\widehat A = \widehat D;\,\widehat B = \widehat E = 55^\circ ;\widehat C\, = \widehat F.\)

Xét tam giác \(ABC\) có \(\widehat A + \widehat B = 130^\circ  \Rightarrow \widehat A = 130^\circ  - \widehat B\)\( = 130^\circ  - 55^\circ  = 75^\circ \)

Lại có $\widehat A + \widehat B + \widehat C = 180^\circ  \Rightarrow \widehat C = 180^\circ  - \left( {\widehat A + \widehat B} \right)$\( = 180^\circ  - 130^\circ  = 50^\circ .\)

Vậy \(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)

Đáp án đúng là c