Giải 8. Bài 3: Phép trừ và phép chia Toán học Lớp 6 | Hướng Dẫn Giải Chân trời sáng tạo Chi Tiết

Đề bài

Câu 1

Phép tính $x - 5$ thực hiện được khi

$x < 5$
$x \ge 5$
$x < 4$
$x = 3$

Câu 2

Cho phép tính $231 - 87$. Chọn câu đúng.

$x < 10$
$x \ge 10$
$x < 9$
$x = 8$

Câu 3

Cho phép tính $x:3 = 6$, khi đó thương của phép chia là

$231$ là số trừ
$87$ là số bị trừ
$231$ là số bị trừ
$87$ là hiệu

Câu 4

Tính 1 454-997

$117$ là số trừ
$564$ là số bị trừ
$117$ là số bị trừ
$447$ là hiệu

Câu 5

Trong phép chia có dư $a$ chia cho $b,$ trong đó $b \ne 0,$ ta luôn tìm được đúng hai số tự nhiên $q$ và $r$ duy nhất sao cho:

$a = b.q + r$

Khẳng định nào sau đây đúng?

$x$
$6$
$3$
$18$

Câu 6

Biểu diễn phép chia $445:13$ dưới dạng $a = b.q + r$ trong đó $0 \le r < b$

Câu 7

Trong các phép chia sau, có bao nhiêu phép chia có dư?

144:3

144:13

144:33

144:30

$r \ge b$
$0 < b < r$
$0 < r < b$
$0 \le r < b$

Câu 8

Hình ảnh sau minh họa cho phép toán nào?

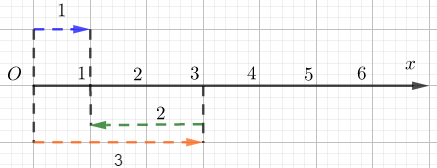
$445 = 13.34 + 3$
$445 = 13.3 + 34$
$445 = 34.3 + 13$
$445 = 13.34$

Câu 9

Dạng tổng quát của số tự nhiên chia hết cho $3$ là:

$1442 = 13.110 + 12$
$1442 = 13.111 + 12$
$1442 = 13.120 + 11$
$1442 = 13.110 + 11$

Câu 10

Dạng tổng quát của số tự nhiên chia cho $5$ dư $2$ là

Câu 11

Tình nhanh $49.15 - 49.5$ ta được kết quả là

3 và 12
12 và 3
11 và 12
12 và 11

Câu 12

Kết quả của phép tính $12.100 + 100.36 - 100.19$ là

0 và 1
1 và 2
52 và 1701
1701 và 52

Đáp án

Câu 1

Phép tính $x - 5$ thực hiện được khi $x \ge 5.$

Đáp án đúng là b

Câu 2

Phép tính $x - 10$ thực hiện được khi $x \ge 10.$

Đáp án đúng là b

Câu 3

Trong phép trừ $231 - 87$ thì $231$ là số bị trừ và $87$ là số trừ nên C đúng.

Đáp án đúng là c

Câu 4

Ta có: $564 - 117 = 447$

Khi đó $564$ là số bị trừ; $117$ là số trừ và $447$ là hiệu nên A, B, D đúng, C sai.

Đáp án đúng là c

Câu 5

Phép chia $x:3 = 6$ có $x$ là số bị chia; $3$ là số chia và $6$ là thương.

Nên thương của phép chia là $6.$

Đáp án đúng là b

Câu 6

1 454-997 = (1 454+3)-(997+3)

= 1 457-1 000=457

Đáp án đúng là c

Câu 7

Khi chia a cho b, trong đó $b \ne 0,$ ta luôn tìm được đúng hai số tự nhiên $q$ và $r$ duy nhất sao cho:

$a = b.q + r$ trong đó $0 \le r < b$

Phép chia a cho b là phép chia có dư nên $r \ne 0$

Vậy $0 < r < b$.

Đáp án đúng là c

Câu 8

Số bị chia là $b = 445$, số chia là $b = 13$ thương $q = 34$, số dư là $r = 3$. Ta biểu diễn phép chia như sau: $445 = 13.34 + 3$

Đáp án đúng là a

Câu 9

Ta có:

$a = 1442,b = 13,q = 110,r = 12$

Vậy $1442 = 13.110 + 12$

Đáp án đúng là a

Câu 10

Vậy có 3 phép chia có dư

Đáp án đúng là c

Câu 11

Vậy $1095=91.12+3$

Thương và số dư lần lượt là 12 và 3.

Đáp án đúng là b